
����Ŀ��������С����Ƶ�����һ��30�������ij߹���ͼ���̣�
��֪��ֱ��AB��ֱ��AB��һ��P��
������ֱ��AB��һ��C��ʹ�á�PCB��30����
������
����ֱ��AB��ȡһ��M��
���Ե�PΪԲ�ģ�PMΪ�뾶��������ֱ��AB���ڵ�M��N��
�۷ֱ���M��NΪԲ�ģ�PMΪ�뾶��������ֱ��AB�·��������ڵ�Q��
������PQ����AB�ڵ�O��
���Ե�PΪԲ�ģ�PQΪ�뾶��������ֱ��AB�ڵ�C�ҵ�C�ڵ�O����࣮���PCB�����������Ľǣ�
����С����Ƶij߹���ͼ���̣�
��1��ʹ��ֱ�ߺ�Բ�油ȫͼ�Σ���������ͼ�ۼ���
��2����������֤����
֤������PM��PN��QM��QN��
���ı���PMQN���� ����
��PQ��MN��PQ��2PO���� ����������д�������ݣ�
����Rt��POC�У�sin��PCB��![]() ���� ������д��ֵ��
���� ������д��ֵ��
���PCB��30����

���𰸡���1������������2�����Σ����ζԽ����ഹֱƽ�֣�![]() ��
��
��������
��1������ͼ����������ͼ���裬��ȫͼ�Σ�������ͼ�ۼ���
��2���������ε��ж������ʣ������Ƶ��ı���PMQN�����Σ����ζԽ����ഹֱƽ�֣��ɵ�PQ��MN��PQ��2PO���������Һ���������������Ľ���30��ǣ�
��1����ͼ��Ϊ��ȫ��ͼ�Σ�
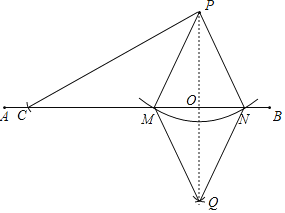
��2����������֤����
��PM��PN��QM��QN��
���ı���PMQN�����Σ�
��PQ��MN��PQ��2PO�����ζԽ����ഹֱƽ�֣���
����Rt��POC��sin��PCB��![]() ��
��
���PCB��30����
�ʴ�Ϊ�����Σ����ζԽ����ഹֱƽ�֣�![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
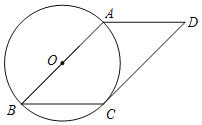
����Ŀ����ͼ����ABCD�У���B��45������Cǡ������ABΪֱ���ġ�O�ϣ�
��1����֤��CD�ǡ�O�����ߣ�
��2������BD����AB��8����BD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ![]() �У�������
�У�������![]() ����x�ύ��A��B����(��A�ڵ�B�����)��
����x�ύ��A��B����(��A�ڵ�B�����)��
��1�����A�͵�B�����ꣻ
��2������P��m��n�����������ϵ�һ�㣬����P��x��Ĵ��ߣ�����Ϊ��D��
����![]() �������£���
�������£���![]() ʱ��n��ȡֵ��Χ��
ʱ��n��ȡֵ��Χ��![]() ���������ߵı���ʽ��
���������ߵı���ʽ��
����D�����꣨4��0������![]() ʱ����a��ȡֵ��Χ.
ʱ����a��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
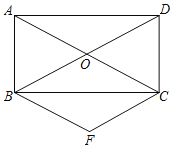
����Ŀ����ͼ������ABCD�ĶԽ���AC��BD�ཻ�ڵ�O����B����BF��AC����C����CF��BD��BF��CF�ཻ�ڵ�F��
��1����֤���ı���BFCO�����Σ�
��2������OF��DF����AB��2��tan��OFD��![]() ����AC�ij���
����AC�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
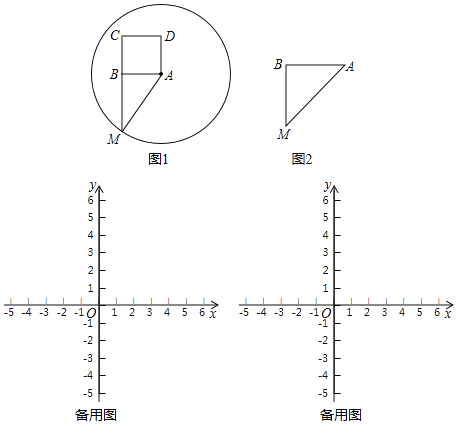
����Ŀ���ڡ�ABM�У���ABM��90������ABΪһ�����ABM�������������ABCD����AΪԲ�ģ�AMΪ�뾶����A�����dz�������ABCDΪ��A�������ڡ�ABM���Ѻ��������������������ABCDǡ�����ڡ�A���ڲ�����Բ�ϣ������dz�������ABCDΪ��A�������ڡ�ABM�ľ����Ѻ��������������磬ͼ1��������ABCD�ǡ�A�������ڡ�ABM���Ѻ�����������
��1��ͼ2�У���ABM�У�BA��BM����ABM��90������ͼ�л�����A�������ڡ�ABM���Ѻ�������ABCD����
��2������A�ڷ���������y��![]() ��k��0��x��0���ϣ����ĺ�������2������A��AB��y����B����������ABCDΪ��A�������ڡ�ABO�ľ����Ѻ�������������k��ȡֵ��Χ��
��k��0��x��0���ϣ����ĺ�������2������A��AB��y����B����������ABCDΪ��A�������ڡ�ABO�ľ����Ѻ�������������k��ȡֵ��Χ��
��3������A��ֱ��y����x+2�ϵ�һ�����㣬����A��AB��y����B����������ABCDΪ��A�������ڡ�ABO�ľ����Ѻ����������������A�ĺ�����m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
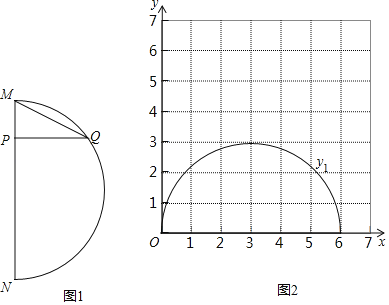
����Ŀ����ͼ1���ڻ�MN����MN����ɵ�ͼ���У�P����MN��һ���㣬����P����MN�Ĵ��ߣ�����MN�ڵ�Q������MQ����֪MN��6cm����M��P�����ľ���Ϊxcm��P��Q�����ľ���Ϊy1cm��M��Q�����ľ���Ϊy2cm��С������ѧϰ�����ľ��飬�ֱ�Ժ���y1��y2���Ա���x�ı仯���仯�Ĺ��ɽ�����̽����������С����̽�����̣��벹��������
��1�������±����Ա���x��ֵ����ȡ�㡢��ͼ���������ֱ�õ���y1��y2��x�ļ����Ӧֵ��x/cm��
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y1/cm | 0 | 2.24 | 2.83 | 3.00 | 2.83 | 2.24 | 0 |
y2/cm | 0 | 2.45 | 3.46 | 4.24 | m | 5.48 | 6 |
�ϱ���m��ֵΪ�� ������������λС����
��2����ͬһƽ��ֱ������ϵxOy��ͼ2���У�����y1��ͼ����ͼ�����������ȫ��ı���y2������ֵ����Ӧ�ĵ㣨x��y2��������������y2��ͼ��
��3����Ϻ���ͼ������⣺����MPQ��һ������30��ʱ��MP�ij���ԼΪ�� ��cm����������λС����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCD�У�AC��BD���ڵ�O����AO��BO��
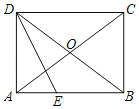
��1����֤���ı���ABCD�Ǿ��Σ�
��2����ADB�Ľ�ƽ����DE��AB�ڵ�E����AD��3��tan��CAB��![]() ʱ����AE�ij���
ʱ����AE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
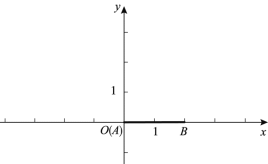
����Ŀ����ƽ��ֱ������ϵ![]() �У���
����![]() ��������
��������![]() �ϴ��ڵ�
�ϴ��ڵ�![]() ��ʹ��
��ʹ��![]() ����
����![]() Ϊ���ĵ��������Σ��ͳƵ�
Ϊ���ĵ��������Σ��ͳƵ�![]() Ϊ�߶�
Ϊ�߶�![]() ��������
��������![]() �ĵ����㣮
�ĵ����㣮
(1)��ͼ�� ![]() ��
��
����![]() �����߶�
�����߶�![]() ��������
��������![]() �ĵ������������_____��
�ĵ������������_____��
����![]() �����߶�
�����߶�![]() ��������
��������![]() �ĵ������������С��1����
�ĵ������������С��1����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
(2) ��![]() ��������
��������![]() ��ֻ����һ���߶�
��ֻ����һ���߶�![]() ��������
��������![]() �ĵ����㣬��
�ĵ����㣬��![]() ��ȡֵ��Χ��__________��
��ȡֵ��Χ��__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
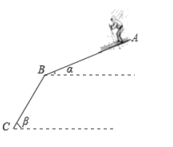
����Ŀ��2022���ڱ������ٰ��24�춬�����˻ᣬ�ܶ�ѧУ����չ�˱�ѩ��Ŀѧϰ����ͼ����ѩ�����AB��BC��������ɣ�AB��BC�ij��ȶ�Ϊ200�ף�һλͬѧ�˻�ѩ���ش˹����A�㻬����C�㣬��AB��ˮƽ��ļн���Ϊ20����BC��ˮƽ��ļн���Ϊ45���������½��ĸ߶�Ϊ�����ף�������������������ο�����sin20���0.342��cos20���0.940��tan20���0.364��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com