
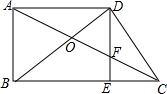
 如图,在直角梯形ABCD中,∠BAD=90°,AD∥BC,对角线AC,BD相交于点O,过D作DE⊥BC,交AC于点F.
如图,在直角梯形ABCD中,∠BAD=90°,AD∥BC,对角线AC,BD相交于点O,过D作DE⊥BC,交AC于点F.分析 (1)四边形OECD是梯形,理由是:如图1,根据三个角是直角的四边形是矩形先证明四边形ABED是矩形,得AB∥DF,得比例式:$\frac{OF}{AO}=\frac{OD}{OB}$,根据已知的OF•AD=EC•AO,化成比例式后得:$\frac{OF}{AO}=\frac{EC}{AD}$,则
$\frac{EC}{BE}=\frac{OD}{OB}$,则OE∥DC,又因为OD与EC不平行,得四边形OECD是梯形;
(2)先证明△DFC∽△BOC,得∠BOC=∠DFC,则∠DOF=∠DFO,最后得AB=BO;再证明△ADF∽△CBA,得比例式,等量代换后化成乘积式得结论.
解答 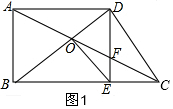 证明:(1)四边形OECD是梯形,理由是:
证明:(1)四边形OECD是梯形,理由是:
如图1,∵OF•AD=EC•AO,
∴$\frac{OF}{AO}=\frac{EC}{AD}$,
∵AD∥BC,∠BAD=90°,
∴∠ABE=180°-90°=90°,
∵DE⊥BC,
∴∠BED=90°,
∴∠BAD=∠ABE=∠BED=90°,
∴四边形ABED是矩形,
∴AB∥DF,AD=BE,
∴$\frac{OF}{AO}=\frac{OD}{OB}$,
∴$\frac{EC}{AD}=\frac{OD}{OB}$,
∵AD=BE,
∴$\frac{EC}{BE}=\frac{OD}{OB}$,
∴OE∥CD,
由图形可知:直线DO与直线CE交于点B,即OD与EC不平行,
∴四边形OECD是梯形;
(2)如图2,∵BD⊥CD,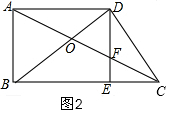
∴∠BDE+∠EDC=90°,
∵∠ABE=90°,
∴∠ABD+∠DBE=90°,
∵AB∥DE,
∴∠ABD=∠BDE,
∴∠EDC=∠DBE,
∵AD∥BC,
∴∠DAC=∠ACB,
∵AD=BE,BE=DC,
∴AD=DC,
∴∠DAC=∠DCA,
∴∠DCA=∠ACB,
∴△DFC∽△BOC,
∴∠BOC=∠DFC,
∴∠DOF=∠DFO,
∵∠AOB=∠DOF,∠BAO=∠DFO,
∴∠AOB=∠BAO,
∴AB=BO,
∵∠DAC=∠ACB,∠ADF=∠ABC=90°,
∴△ADF∽△CBA,
∴$\frac{AF}{AC}=\frac{DF}{AB}$,
∴$\frac{AF}{AC}=\frac{DF}{BO}$,
∴BO•AF=AC•DF.
点评 本题考查了相似三角形、直角梯形和梯形的性质及判定,此类题有难度;一般情况下判定一个四边形是梯形时,要注意证明两个结论:①一组对边平行,②另一组对边不平行;此题有几点得出比较关键:①BE=CD,通过AD的转化,变为同一个三角形中,可以利用等边对等角得角的关系;②AB=BO:通过证得△DOF为等腰三角形,而等腰三角形的得出,又通过证明△DFC∽△BOC,根据相似性质得:第三个角相等得出;从而使最后的问题得以解决.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知如图,△ABC中,∠C=90°,AB=10,BC=6,
已知如图,△ABC中,∠C=90°,AB=10,BC=6,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com