练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    如图，正方形A，B，C，D的顶点ABCD都在坐标轴上，已知OA=OB=OC=OD=
    		2
    ，请分别写出顶点A，B，C，D的坐标．
    考点：正方形的性质,坐标与图形性质
    专题：
    分析：根据线段OA、OB、OC、OD的长度，可直接得出A、B、C、D的坐标．
    解答：解：∵OA=OB=OC=OD=
    		2
    ，
    ∴A（-
    		2
    ，0），B（0，
    		2
    ），C（
    		2
    ，0），D（0，-
    		2
    ）．
    点评：本题主要考查点的坐标的意义，掌握线段长度与坐标的关系是解题的关键，注意坐标轴上的点的坐标的特点．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

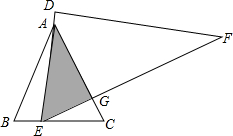    如图，等边△ABC中，AB=6，将一直角三角板DEF的60°角的顶点E置于边BC上移动（不与B、C重合），移动过程中，始终满足直角边DE经过点A，斜边EF交AC于点G．
    （1）求证：△ABE∽△ECG；
    （2）在移动过程中，线段CG有没有最大值？若有，请求出，若没有，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，已知∠BAC=90°，AD⊥BC，∠1=∠2，EF⊥BC，FM⊥AC，说明FM=FD的理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图是一个多边形，求∠A1+∠A2+∠A3+…+∠A23+∠A24的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，在△ABC中，点D在BC上，BD：DC=1：2，点E在AB上，AE：EB=3：2，AD，CE相交于F，则AF：FD=
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    有一块形状为平行四边形的铁片，用AB表示较长的一边，AD、BC表示较短的边，现有AB=2AD．现在想用这块铁片截一个直角三角形，并且希望以AB为斜边，直角顶点在CD上，问此想法是否可行？如果可行的话，请说明应该怎样截；如果不行，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，四边形ABCD是矩形，四边形AECF是菱形，若AB=4，BC=8，求菱形AECF的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，△ABC中，AD是∠BAC的平分线，AD的垂直平分线AD交于点E，交BC的延长线于点F．试说明：△ABF∽△CAF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，小明在河岸的A处观察对岸C处的一棵树，视线与河岸30°角；同时，小亮在距小明100米的河岸B观察对岸D处的一棵树，视线与河岸成75°角．已知河宽90米，且两岸平行，求河对岸C、D两棵树的距离．（参考数据：
    		3
    ≈1.7，
    		2
    ≈1.4）

    查看答案和解析>>

    同步练习册答案