
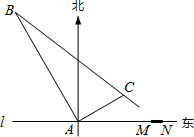
 偏东60°,且与A相距8
偏东60°,且与A相距8| 3 |
| 3 |
| AB2+AC2 |
402+(8
|
| 7 |
16
| ||
| 80 |
| 7 |
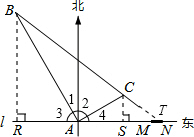 ∵∠2=60°,
∵∠2=60°,| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| ||
| 2 |
| 3 |
| 1 |
| 2 |
| ST |
| RT |
| CS |
| BR |
| ST |
| ST+20+12 |
4
| ||
20
|


科目:初中数学 来源: 题型:
 (2012•乐山)如图,在东西方向的海岸线l上有一长为1千米的码头MN,在码头西端M的正西方向30 千米处有一观察站O.某时刻测得一艘匀速直线航行的轮船位于O的北偏西30°方向,且与O相距20
(2012•乐山)如图,在东西方向的海岸线l上有一长为1千米的码头MN,在码头西端M的正西方向30 千米处有一观察站O.某时刻测得一艘匀速直线航行的轮船位于O的北偏西30°方向,且与O相距20| 3 |
| 2 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•广州)如图,在东西方向的海岸线MN上有A、B两艘船,均收到已触礁搁浅的船P的求救信号,已知船P在船A的北偏东58°方向,船P在船B的北偏西35°方向,AP的距离为30海里.
(2013•广州)如图,在东西方向的海岸线MN上有A、B两艘船,均收到已触礁搁浅的船P的求救信号,已知船P在船A的北偏东58°方向,船P在船B的北偏西35°方向,AP的距离为30海里.查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•铁岭)如图,在东西方向的海岸线上有A、B两个港口,甲货船从A港沿北偏东60°的方向以4海里/小时的速度出发,同时乙货船从B港沿西北方向出发,2小时后相遇在点P处,问乙货船每小时航行
(2012•铁岭)如图,在东西方向的海岸线上有A、B两个港口,甲货船从A港沿北偏东60°的方向以4海里/小时的速度出发,同时乙货船从B港沿西北方向出发,2小时后相遇在点P处,问乙货船每小时航行| 2 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在东西方向的海岸线上有A、B两个港口,甲货船从A港沿北偏东60°的方向以4海里/小时的速度出发,同时乙货船从B港沿西北方向出发,2小时后相遇在点P处,问乙货船每小时航行多少海里?
如图,在东西方向的海岸线上有A、B两个港口,甲货船从A港沿北偏东60°的方向以4海里/小时的速度出发,同时乙货船从B港沿西北方向出发,2小时后相遇在点P处,问乙货船每小时航行多少海里?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com