
【题目】某数学老师为了了解学生在数学学习中常见错误的纠正情况,收集整理了学生在作业和考试中的常见错误,编制了10道选择题,每题3分,对他所教的初三(1)班、(2)班进行了检测,如图表示从两班各随机抽取的10名学生的得分情况.
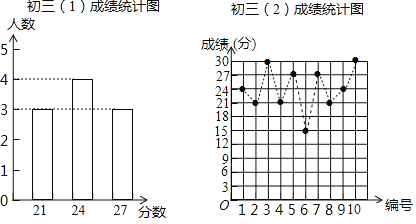
(1)利用图中提供的信息,补全下表:
班级 | 平均数/分 | 中位数/分 | 众数/分 |
初三(1)班 | __________ | 24 | ________ |
初三(2)班 | 24 | _________ | 21 |
(2)若把24分以上(含24分)记为“优秀”,两班各40名学生,请估计两班各有多少名学生成绩优秀;
(3)观察上图的数据分布情况,请通过计算说明哪个班的学生纠错的得分更稳定.
【答案】(1)见解析;(2)(1)班优秀学生约是28人;(2)班优秀学生约是24人;(3)见解析.
【解析】
(1)根据平均数、中位数和众数的定义进行解答即可;
(2)找到样本中24分和24分人数所占的百分数,用样本平均数估计总体平均数;
(3)计算出两个班的方差,方差越小越稳定.
(1)初三(1)班平均分:![]() (21×3+24×4+27×3)=24(分);
(21×3+24×4+27×3)=24(分);
有4名学生24分,最多,故众数为24分;
把初三(2)班的成绩从小到大排列,则处于中间位置的数为24和24,故中位数为24分,
填表如下:
班级 | 平均数/分 | 中位数/分 | 众数/分 |
初三(1)班 | 24 | 24 | 24 |
初三(2)班 | 24 | 24 | 21 |
故答案为:24,24,24;
(2)初三(1)班优秀学生约是![]() =28(人);
=28(人);
初三(2)班优秀学生约是![]() =24(人).
=24(人).
(3)![]() [
[![]() ×3+
×3+![]() ×4+
×4+![]() ×3]
×3]![]() (27+27)
(27+27)![]() ;
;![]() [
[![]() ]
]
![]()
![]() 198
198![]() ;
;
∵![]() ,
,
∴初三(1)班的学生纠错的得分更稳定.


科目:初中数学 来源: 题型:
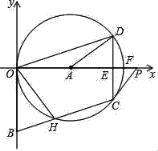
【题目】如图,⊙A过OBCD的三顶点O、D、C,边OB与⊙A相切于点O,边BC与⊙O相交于点H,射线OA交边CD于点E,交⊙A于点F,点P在射线OA上,且∠PCD=2∠DOF,以O为原点,OP所在的直线为x轴建立平面直角坐标系,点B的坐标为(0,﹣2).
(1)若∠BOH=30°,求点H的坐标;
(2)求证:直线PC是⊙A的切线;
(3)若OD=![]() ,求⊙A的半径.
,求⊙A的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题发现)
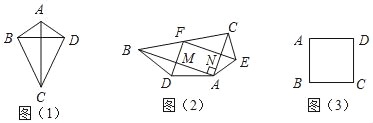
(1)如图(1)四边形ABCD中,若AB=AD,CB=CD,则线段BD,AC的位置关系为 ;
(拓展探究)
(2)如图(2)在Rt△ABC中,点F为斜边BC的中点,分别以AB,AC为底边,在Rt△ABC外部作等腰三角形ABD和等腰三角形ACE,连接FD,FE,分别交AB,AC于点M,N.试猜想四边形FMAN的形状,并说明理由;
(解决问题)
(3)如图(3)在正方形ABCD中,AB=2![]() ,以点A为旋转中心将正方形ABCD旋转60°,得到正方形AB'C'D',请直接写出BD'平方的值.
,以点A为旋转中心将正方形ABCD旋转60°,得到正方形AB'C'D',请直接写出BD'平方的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016浙江省丽水市)如图,在菱形ABCD中,过点B作BE⊥AD,BF⊥CD,垂足分别为点E,F,延长BD至G,使得DG=BD,连结EG,FG,若AE=DE,则![]() =____.
=____.

查看答案和解析>>
科目:初中数学 来源: 题型:
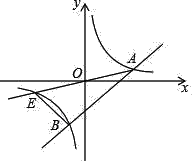
【题目】如图,直线y=kx+b(k为常数,k≠0)与双曲线y=![]() (m为常数,m>0)的交点为A(4,1)、B(﹣1,﹣4),连接AO并延长交双曲线于点E,连接BE.
(m为常数,m>0)的交点为A(4,1)、B(﹣1,﹣4),连接AO并延长交双曲线于点E,连接BE.
(1)分别求出这两个函数的表达式;
(2)求△ABE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
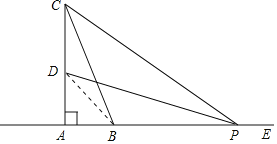
【题目】如图,在△ABC中,∠BAC=90°,AB=5cm,BC=13cm,点D在线段AC上,且CD=7cm,动点P从距B点15cm的E点出发,以每秒2cm的速度沿射线EA的方向运动,时间为t秒.
(1)求AD的长.
(2)用含有t的代数式表示AP的长.
(3)在运动过程中,是否存在某个时刻,使△ABC与△ADP全等?若存在,请求出t值;若不存在,请说明理由.
(4)直接写出t=______秒时,△PBC为等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
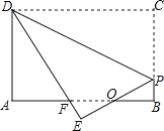
【题目】如图,矩形纸片ABCD,AB=4,BC=3,点P在BC边上,将△CDP沿DP折叠,点C落在点E处,PE.、DE分别交AB于点O、F,且OP=OF,则BP的长为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com