
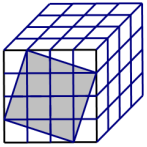
 魔方,又叫魔术方块,也称鲁比克方块,是匈牙利布达佩斯建筑学院厄尔诺•鲁比克教授在1974年发明的.魔方与中国人发明的“华容道”,法国人发明的“独立钻石”一同被称为智力游戏界的三大不可思议.如图是一个4阶魔方,又称“魔方的复仇”,由四层完全相同的64个小立方体组成,体积为64cm3.
魔方,又叫魔术方块,也称鲁比克方块,是匈牙利布达佩斯建筑学院厄尔诺•鲁比克教授在1974年发明的.魔方与中国人发明的“华容道”,法国人发明的“独立钻石”一同被称为智力游戏界的三大不可思议.如图是一个4阶魔方,又称“魔方的复仇”,由四层完全相同的64个小立方体组成,体积为64cm3. 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
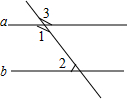 如图,已知直线a∥b,∠3=135°,求∠1、∠2的度数,请你填空或填写理由.
如图,已知直线a∥b,∠3=135°,求∠1、∠2的度数,请你填空或填写理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
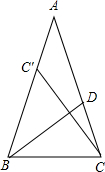 如图,D是△ABC的边AC上一点,AB=AC,BD=BC,将△BCD沿BD折叠,顶点C恰好落在一边上的C′处.
如图,D是△ABC的边AC上一点,AB=AC,BD=BC,将△BCD沿BD折叠,顶点C恰好落在一边上的C′处.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
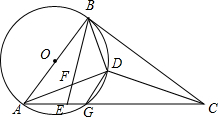 如图:AB是⊙O的直径,AC交⊙O于G,E是AG上一点,D为△BCE内心,BE交AD于F,且∠DBE=∠BAD.
如图:AB是⊙O的直径,AC交⊙O于G,E是AG上一点,D为△BCE内心,BE交AD于F,且∠DBE=∠BAD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com