
分析 (1)根据每个括号内的算式和的变化可找出变化规律“$\frac{1}{n}$+$\frac{2}{n}$+…+$\frac{n-1}{n}$=$\frac{1}{2}$(n-1)”,依此规律即可得出结论;
(2)根据每个分式的变化可找出变化规律“$\frac{1}{1+2+3+…+n}$=$\frac{2}{n(n+1)}$=2×($\frac{1}{n}$-$\frac{1}{n+1}$)”,依此规律即可得出结论.
解答 解:(1)∵$\frac{1}{2}$=$\frac{1}{2}$,$\frac{1}{3}$+$\frac{2}{3}$=2×$\frac{1}{2}$,$\frac{1}{4}$+$\frac{2}{4}$+$\frac{3}{4}$=3×$\frac{1}{2}$,$\frac{1}{5}$+$\frac{2}{5}$+$\frac{3}{5}$+$\frac{4}{5}$=4×$\frac{1}{2}$,…,
∴$\frac{1}{n}$+$\frac{2}{n}$+…+$\frac{n-1}{n}$=$\frac{1}{2}$(n-1),
∴$\frac{1}{2}$+(${\frac{1}{3}$+$\frac{2}{3}}$)+(${\frac{1}{4}$+$\frac{2}{4}$+$\frac{3}{4}}$)+…+(${\frac{1}{60}$+$\frac{2}{60}$+…+$\frac{59}{60}}$)=$\frac{1}{2}$+2×$\frac{1}{2}$+3×$\frac{1}{2}$+…+59×$\frac{1}{2}$=(1+2+3+…+59)×$\frac{1}{2}$=$\frac{(1+59)×59}{2}$×$\frac{1}{2}$=885.
故答案为:885.
(2)∵$\frac{1}{1+2}$=$\frac{2}{2×3}$=2×($\frac{1}{2}$-$\frac{1}{3}$),$\frac{1}{1+2+3}$=$\frac{2}{3×4}$=2×($\frac{1}{3}$-$\frac{1}{4}$),$\frac{1}{1+2+3+4}$=$\frac{2}{4×5}$=2×($\frac{1}{4}$-$\frac{1}{5}$),…,
∴$\frac{1}{1+2+3+…+n}$=$\frac{2}{n(n+1)}$=2×($\frac{1}{n}$-$\frac{1}{n+1}$),
∴1+$\frac{1}{1+2}$+$\frac{1}{1+2+3}$+…+$\frac{1}{1+2+3+…+100}$=1+2×($\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{100}$-$\frac{1}{101}$)=1+2×($\frac{1}{2}$-$\frac{1}{101}$)=$\frac{200}{101}$.
故答案为:$\frac{200}{101}$.
点评 本题考查了规律型中数字的变化类,根据数和分式的变化找出变化规律是解题的关键.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:填空题
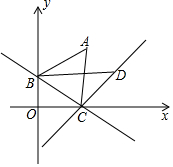 如图,直线y=-$\frac{\sqrt{3}}{3}$x+2与x轴交于点C,与y轴交于点B,点A在第一象限内,△ABC是正三角形,点D是直线y=x-2$\sqrt{3}$上第一象限内一点,△DBC和△ABC面积相等,则点D的坐标是(6,6-2$\sqrt{3}$).
如图,直线y=-$\frac{\sqrt{3}}{3}$x+2与x轴交于点C,与y轴交于点B,点A在第一象限内,△ABC是正三角形,点D是直线y=x-2$\sqrt{3}$上第一象限内一点,△DBC和△ABC面积相等,则点D的坐标是(6,6-2$\sqrt{3}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com