
【题目】中踏集团销售某种商品,每件进价为10元。在销售过程中发现,平均每天的销售量y(件)与销售价x(元/件)(不低于进价)之间的关系可近似的看做一次函数:![]() ;
;
(1)求中踏集团平均每天销售这种商品的利润w(元)与销售价x之间的函数关系式;
(2)当这种商品的销售价为多少元时,可以获得最大利润,最大利润是多少?
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦BC=2cm,F是弦BC的中点,∠ABC=60°.若动点E以2cm/s的速度从A点出发沿着A→B→A方向运动,设运动时间为t(s)(0≤t<3),连接EF,当△BEF是直角三角形时,t(s)的值为【 】

A.![]() B.1 C.
B.1 C.![]() 或1 D.
或1 D.![]() 或1或
或1或![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC三个顶点的坐标分别为A(2,4),B(1,1),C(4,3).
(1)请画出△ABC关于x轴对称的△A1B1C1,并写出点A1的坐标;
(2)请画出△ABC绕点B逆时针旋转90°后的△A2BC2;
(3)求出(2)中C点旋转到C2点所经过的路径长(结果保留根号和π);
(4)求出(2)△A2BC2的面积是多少.

查看答案和解析>>
科目:初中数学 来源: 题型:
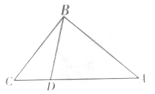
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 为
为![]() 边上的动点,点
边上的动点,点![]() 从点
从点![]() 出发,沿边
出发,沿边![]() 向点
向点![]() 运动,当运动到点
运动,当运动到点![]() 时停止,若设点
时停止,若设点![]() 运动的时间为
运动的时间为![]() 秒,点
秒,点![]() 运动的速度为每秒2个单位长度.
运动的速度为每秒2个单位长度.

(1)当![]() 时,
时,![]() = ,
= ,![]() = ;
= ;
(2)求当![]() 为何值时,
为何值时,![]() 是直角三角形,说明理由;
是直角三角形,说明理由;
(3)求当![]() 为何值时,
为何值时,![]() ,并说明理由.
,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-3,2)、B(0,4)、C(0,2),
(1)画出△ABC关于点C成中心对称的△A1B1C;
(2)平移△ABC:若点A的对应点A2的坐标为(0,-4),画出平移后对应的△A2B2C2;
(3)△A1B1C和△A2B2C2关于某一点成中心对称,则对称中心的坐标为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
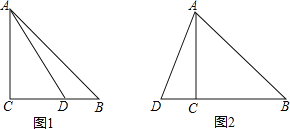
【题目】在△ABC中,∠C=90°,AC=BC,点D在射线BC上(不与点B、C重合),连接AD,将AD绕点D顺时针旋转90°得到DE,连接BE.
(1)如图1,点D在BC边上.
①依题意补全图1;
②作DF⊥BC交AB于点F,若AC=8,DF=3,求BE的长;
(2)如图2,点D在BC边的延长线上,用等式表示线段AB、BD、BE之间的数量关系(直接写出结论).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展以感恩教育为主题的艺术活动,举办了四个项目的比赛,它们分别是演讲、唱歌、书法、绘画。要求每位同学必须参加,且限报一项活动。以九年级(1)班为样本进行统计,并将统计结果绘成如图1、图2所示的两幅统计图。请你结合图示所给出的信息解答下列问题。

(1)求出参加绘画比赛的学生人数占全班总人数的百分比?
(2)求出扇形统计图中参加书法比赛的学生所在扇形圆心角的度数?
(3)若该校九年级学生有600人,请你估计这次艺术活动中,参加演讲和唱歌的学生各有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com