
分析 (1)根据tan∠DCO=$\frac{1}{2}$设OD=a,OC=2a,根据S△ADE=4列式求出a的值,分情况讨论:分别写出D、C、A三点的坐标,对应求出解析式即可;
(2)分两种情况计算面积:先计算点B的坐标,过B作BF⊥x轴于F,求出BF的长为2,①当k1>0,k2>0时,如图3,根据S△AA′B=S△ADA′+S△A′DB,代入计算即可;②当k1<0,k2<0时,如图4,过B作BF⊥x轴于F,同理可求得△AA′B的面积.
解答  解:(1)∵tan∠DCO=$\frac{1}{2}$.
解:(1)∵tan∠DCO=$\frac{1}{2}$.
∴$\frac{OD}{OC}$=$\frac{1}{2}$
设OD=a,OC=2a
∵点O为DE中点,OC∥AE
∴OD=OE,△DOC∽△DEA
∴$\frac{{S}_{△DOC}}{{S}_{△DEA}}$=$\frac{1}{4}$
∵S△ADE=4,
∴S△DOC=1
则$\frac{1}{2}$OC•OD=1
$\frac{1}{2}$a•2a=1,a=±1,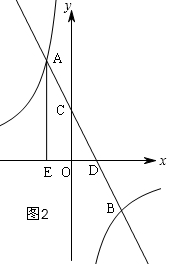
分两种情况:
①如图1,D(-1,0)、C(0,2)、A(1,4),
把D(-1,0)、C(0,2)代入y1=k1x+b中得:$\left\{\begin{array}{l}{-{k}_{1}+b=0}\\{b=2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{k}_{1}=2}\\{b=2}\end{array}\right.$,
∴y1=2x+2,
把A(1,4)代入y2=$\frac{{k}_{2}}{x}$得:k2=1×4=4,
∴y2=$\frac{4}{x}$,
②如图2,D(1,0)、C(0,2)、A(-1,4),
把D(1,0)、C(0,2)代入y1=k1x+b中得:$\left\{\begin{array}{l}{{k}_{1}+b=0}\\{b=2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{k}_{1}=-2}\\{b=2}\end{array}\right.$,
∴y1=-2x+2,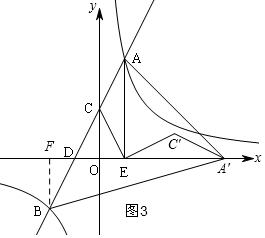
把A(-1,4)代入y2=$\frac{{k}_{2}}{x}$得:k2=-1×4=-4,
∴y2=-$\frac{4}{x}$,
(2)分两种情况:
①当k1>0,k2>0时,如图3,过B作BF⊥x轴于F,
由旋转得:A′E=AE=4,则A′D=OD+OE+A′E=1+1+4=6,
$\left\{\begin{array}{l}{y=2x+2}\\{y=\frac{4}{x}}\end{array}\right.$ 解得:$\left\{\begin{array}{l}{{x}_{1}=-2}\\{{y}_{1}=-2}\end{array}\right.$ $\left\{\begin{array}{l}{{x}_{2}=1}\\{{y}_{2}=4}\end{array}\right.$,
∴B(-2,-2),
∴BF=2,
∴S△AA′B=S△ADA′+S△A′DB,
=$\frac{1}{2}$A′D•AE+$\frac{1}{2}$A′D•BF,
=$\frac{1}{2}$×6×4+$\frac{1}{2}$×6×2,
=18;
②当k1<0,k2<0时,如图4,过B作BF⊥x轴于F,
同理得:BF=2,
则A′D=A′E-OE-OD=4-1-1=2,
∴S△AA′B=S△ADA′+S△A′DB,
=$\frac{1}{2}$A′D•AE+$\frac{1}{2}$A′D•BF,
=$\frac{1}{2}$×2×4+$\frac{1}{2}$×2×2,
=6;
综上所述,△AA′B的面积为18或6.
点评 本题考查了反比例函数和一次函数的交点问题,利用解析式组成方程组,求出解即是交点坐标;同时还考查了坐标与图形变换--旋转,熟练掌握旋转的性质:旋转前后的两线段相等;注意在求三角形面积时,将不规则的三角形化为几个三角形面积的和来求,比较简单.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
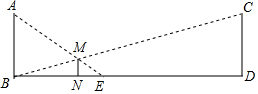 如图,在宽(BD)为24m的马路两旁有两盏路灯(A和C),当小华站在马路上的N处时,由灯C照射的光线影长正好为NB.由灯A照射的光线,影长为NE,现测得NB=6m,NE=2m,小华身高(MN)1.50m,求路灯AB和CD的高度.
如图,在宽(BD)为24m的马路两旁有两盏路灯(A和C),当小华站在马路上的N处时,由灯C照射的光线影长正好为NB.由灯A照射的光线,影长为NE,现测得NB=6m,NE=2m,小华身高(MN)1.50m,求路灯AB和CD的高度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
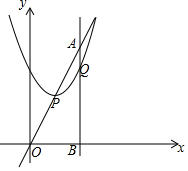 如图,点A(2,4),作AB⊥x铀于点B,抛物线y=x2+bx+c的顶点P在直线OA上,且抛物线交线段AB于点Q,求线段AQ的最大值及此时抛物线的解析式.
如图,点A(2,4),作AB⊥x铀于点B,抛物线y=x2+bx+c的顶点P在直线OA上,且抛物线交线段AB于点Q,求线段AQ的最大值及此时抛物线的解析式.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
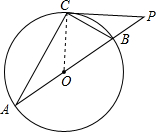 如图,AB是圆O直径,C是圆O上一点,P在AB延长线上,且∠PCB=∠A.
如图,AB是圆O直径,C是圆O上一点,P在AB延长线上,且∠PCB=∠A.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
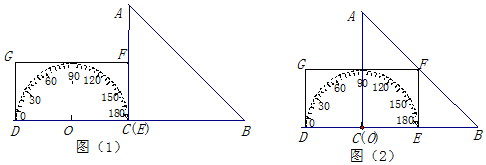
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com