
 随着车辆的增加,交通违规的现象越来越严重,交警对人民路某雷达测速区检测到的一组汽车的时速数据进行整理(速度在30-40含起点值30,不含终点值40),得到其频数及频率如表:
随着车辆的增加,交通违规的现象越来越严重,交警对人民路某雷达测速区检测到的一组汽车的时速数据进行整理(速度在30-40含起点值30,不含终点值40),得到其频数及频率如表:| 数据段 | 频数 | 频率 |
| 30-40 | 10 | 0.05 |
| 40-50 | 36 | c |
| 50-60 | a | 0.39 |
| 60-70 | b | d |
| 70-80 | 20 | 0.10 |
| 总计 | 200 | 1 |
分析 (1)根据第一组的频数是10,对应的频率是0.05即可求得整理的车辆总数,然后根据百分比的意义求解;
(2)根据(1)的结果即可补全直方图;
(3)求得最后两组的和即可.
解答 解:(1)整理的车辆总数是:10÷0.05=200(辆),
则a=200×0.39=78,
c=$\frac{36}{200}$=0.18;
d=1-0.18-0.39-0.10=0.28,
b=200×0.28=56.
故答案是:78;56;0.18;0.28;
(2) ;
;
(3)违章车辆共有56+20=76(辆).
点评 本题考查读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:解答题
 直线y=x-6与x轴、y轴分别交于A、B两点,点E从B点出发,以每秒1个单位长度的速度沿线段BO向O点移动(不考虑点E与B、O两点重合的情况),过点E作EF∥AB,交x轴于点F,将四边形ABEF沿直线EF折叠后,与点A对应的点记作点C,与点B对应的点记作点D,得到四边形CDEF,设点E的运动时间为t秒.
直线y=x-6与x轴、y轴分别交于A、B两点,点E从B点出发,以每秒1个单位长度的速度沿线段BO向O点移动(不考虑点E与B、O两点重合的情况),过点E作EF∥AB,交x轴于点F,将四边形ABEF沿直线EF折叠后,与点A对应的点记作点C,与点B对应的点记作点D,得到四边形CDEF,设点E的运动时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 一个三角形中可以有两个直角 | |
| B. | 一个三角形的三个内角能都大于70° | |
| C. | 一个三角形的三个内角能都小于50° | |
| D. | 三角形中最大的内角不能小于60° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
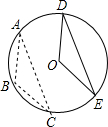 如图,△ABC是⊙O的内接三角形,平移△ABC使点B与圆心O重合,A、C两点恰好落在圆上的D、E两点处.若AC=2$\sqrt{3}$,则平移的距离为2.
如图,△ABC是⊙O的内接三角形,平移△ABC使点B与圆心O重合,A、C两点恰好落在圆上的D、E两点处.若AC=2$\sqrt{3}$,则平移的距离为2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ±2 | B. | ±1 | C. | 1 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com