
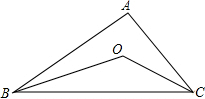
 如图所示,BO,CO分别平分∠ABC和∠ACB.
如图所示,BO,CO分别平分∠ABC和∠ACB.| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:
 如图,已知点A(0,4),B(2,0),点M是线段AB上一动点(不与点、B重合),以M为顶点的抛物线y=(x-m)2+n与直线OA交于点C,求线段AC长度的取值范围.
如图,已知点A(0,4),B(2,0),点M是线段AB上一动点(不与点、B重合),以M为顶点的抛物线y=(x-m)2+n与直线OA交于点C,求线段AC长度的取值范围.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图所示,某人到岛上去探宝,从A处登陆后先往东走8km,又往北走1.5km,遇到障碍后又往西走2.5km,再折回向北走到6.5km处往东一拐,仅走0.5km就找到了宝藏,问登陆点A与宝藏埋藏点B之间的距离是多少?
如图所示,某人到岛上去探宝,从A处登陆后先往东走8km,又往北走1.5km,遇到障碍后又往西走2.5km,再折回向北走到6.5km处往东一拐,仅走0.5km就找到了宝藏,问登陆点A与宝藏埋藏点B之间的距离是多少?查看答案和解析>>
科目:初中数学 来源: 题型:
 阅读下列内容:
阅读下列内容:| 3 |
| AC |
| CD |
| k | ||
(2+
|
| 1 | ||
2+
|
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
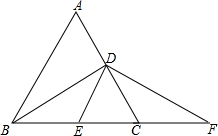 如图,在△ABC中,AB=AC,∠A=60°,BD⊥AC于点D,E为BC的中点,DF⊥DE,交BC的延长线于点F,求证:E,C两点是线段BF的等分点.
如图,在△ABC中,AB=AC,∠A=60°,BD⊥AC于点D,E为BC的中点,DF⊥DE,交BC的延长线于点F,求证:E,C两点是线段BF的等分点.查看答案和解析>>
科目:初中数学 来源: 题型:
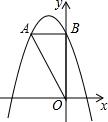 如图,在平面直角坐标系中,O是坐标原点,点A的坐标是(-2,4),过点A作AB⊥y轴,垂足为B,连结OA.
如图,在平面直角坐标系中,O是坐标原点,点A的坐标是(-2,4),过点A作AB⊥y轴,垂足为B,连结OA.查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 2 |
| 4 |
| x |
| A、x3>x2>x1 |
| B、x1>x2>x3 |
| C、x1>x3>x2 |
| D、x3>x1>x2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com