练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    9．已知A=（x+2）2，B=2x（$\frac{1}{2}$x-2），求A-B．

    分析 把A与B代入A-B中，化简即可得到结果．

    解答 解：∵A=（x+2）2，B=2x（$\frac{1}{2}$x-2），
    ∴A-B=（x+2）2-2x（$\frac{1}{2}$x-2）=x2+4x+4-x2+4x=8x+4．

    点评 此题考查了整式的混合运算，熟练掌握运算法则是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

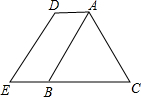    19．如图，在△ABC中，AB=AC，AC+BC=14，将△ABC边沿CB方向向左平移$\frac{1}{2}$BC的长，连接AD、BE、DE，求四边形ACED的周长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．如图：在矩形ABCD中，AB：BC=12：5，BE⊥AC于点E，DF⊥AC于点F，求EF：CE的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    17．若把x2+2x-2=0化为（x+m）2+k=0的形式（m，k为常数），则m+k的值为（　　）
    A．-2B．-4C．2D．4

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．如图，AD是△ABC的外角平分线，且$\frac{AB}{AC}$=$\frac{\sqrt{5}+1}{2}$，求证：C是BD的黄金分割点．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．如图，∠α和∠β的度数满足方程组$\left\{\begin{array}{l}{2∠α+∠β=235°}\\{∠β-∠α=70°}\end{array}\right.$，且CD∥EF，AC⊥AE．
    （1）求∠α与∠β的度数；
    （2）判断AB与CD的位置关系，并说明理由．
    （3）求∠C的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    1．如图，A、B两点分别位于一个池塘的两端，小明想用绳子测量A、B间的距离，但绳子不够长，一位同学帮他想了一个主意：先在地上取一个可以直接到达点A、B的点C，分别在AC、BC上取中点D、E，测得DE=5米，则A、B两点间的距离为10米．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    18．在△ABC中，三条边长分别为a、b、c，以下条件不能证明△ABC是直角三角形的是（　　）
    A．a2=b2+c2B．∠A+∠B=90°
    C．△ABC与直角三角形CDE全等D．（a+b）2=c2

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．小丽驾车从甲地到乙地．设她出发第xmin时的速度为ykm/h，图中的折线表示她在整个驾车过程中y与x之间的函数关系．

    （1）小丽驾车的最高速度是60km/h；
    （2）当20≤x≤40时，求y与x之间的函数关系式，并求出小丽出发第30min时的速度；
    （3）如果汽车每行驶100km耗油10L，那么小丽驾车从甲地到乙地共耗油多少升？

    查看答案和解析>>

    同步练习册答案