Question

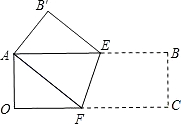
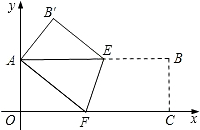
如图所示，将矩形OABC沿AE折叠，使点O恰好落在BC上F处，以CF为边作正方形CFGH，延长BC至M，使CM＝｜CF―EO｜，再以CM、CO为边作矩形CMNO

(1)试比较EO、EC的大小，并说明理由

(2)令，请问m是否为定值？若是，请求出m的值；若不是，请说明理由

(3)在(2)的条件下，若CO＝1，CE＝，Q为AE上一点且QF＝，抛物线y＝mx²+bx+c经过C、Q两点，请求出此抛物线的解析式.

 (4)在(3)的条件下，若抛物线y＝mx²+bx+c与线段AB交于点P，试问在直线BC上是否存在点K，使得以P、B、K为顶点的三角形与△AEF相似?若存在，请求直线KP与y轴的交点T的坐标?若不存在，请说明理由。

Answer 1

（1）EO＞EC，理由如下：

由折叠知，EO=EF，在Rt△EFC中，EF为斜边，∴EF＞EC， 故EO＞EC

（2）m为定值

∵S_{四边形CFGH}=CF²=EF²－EC²=EO²－EC²=(EO+EC)(EO-EC)=CO?(EO-EC)

S_{四边形CMNO}=CM?CO=|CE-EO|?CO=(EO-EC) ?CO

∴

（3）∵CO=1， ∴EF=EO=

∴cos∠FEC= ∴∠FEC=60°，

∴

∴△EFQ为等边三角形，

作QI⊥EO于I，EI=，IQ=

∴IO= ∴Q点坐标为

∵抛物线y=mx²+bx+c过点C(0，1)， Q ，m=1

∴可求得，c=1

∴抛物线解析式为

（4）由（3），

当时，＜AB

∴P点坐标为　

∴BP=AO

方法1：若△PBK与△AEF相似，而△AEF≌△AEO，则分情况如下：

①时，∴K点坐标为或

②时， ∴K点坐标为或

故直线KP与y轴交点T的坐标为



方法2：若△BPK与△AEF相似，由（3）得：∠BPK=30°或60°，过P作PR⊥y轴于R，则∠RTP=60°或30°

①当∠RTP=30°时，

②当∠RTP=60°时，

∴