
【题目】已知:![]() 和
和![]() 都是等边三角形,点
都是等边三角形,点![]() 在边
在边![]() 上,连接
上,连接![]() .
.
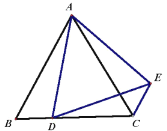
(1)如图1,求证:![]() ;
;
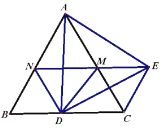
(2)如图2,点![]() 在
在![]() 上,
上,![]() (
(![]() ),连接
),连接![]() 并延长交
并延长交![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() ,在不添加任何辅助线的情况下,请直接写出图2中所有与线段
,在不添加任何辅助线的情况下,请直接写出图2中所有与线段![]() 相等的线段(线段
相等的线段(线段![]() 除外).
除外).
【答案】(1)见解析(2)与线段BD相等的线段有:ME、CM、BN、DN
【解析】
(1)证明△BAD≌△CAE(SAS),可得BD=CE.
(2)如图2中,与线段BD相等的线段有:ME、CM、BN、DN.想办法证明△MCE,△BDN都是等边三角形即可解决问题.
(1)证明:∵△ABC和△ADE都是等边三角形,
∴AB=AC、AD=AE,∠BAC=∠DAE=60°,
∴∠BAC∠DAC=∠DAE∠DAC
即∠BAD=∠CAE,
∴△BAD≌△CAE(SAS),
∴BD=CE.
(2)解:如图2中,与线段BD相等的线段有:ME、CM、BN、DN.
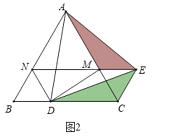
∵△BAD≌△CAE,
∴∠ACE=∠B=60°,
∵∠ADC=60°+∠EDC=60°+∠BAD,
∴∠EDC=∠BAD,
∵∠BAD=∠CAE,
∴∠EDC=∠EAM,
∵MA=CD,AE=DE,
∴△MAE≌△CDE(SAS),
∴EM=EC,
∵∠MCE=60°,
∴△MCE是等边三角形,
∴∠CME=∠AMN=60°,
∵∠MAN=60°,
∴△AMN是等边三角形,
∴AN=AM,
∵AB=AC,
∴BN=CM,
∵BD=EC=CM,
∴BD=BN,
∵∠B=60°,
∴△BND是等边三角形,
∴与线段BD相等的线段有:ME、CM、BN、DN.


科目:初中数学 来源: 题型:
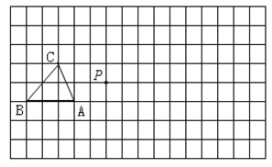
【题目】在下面的正方形网格中,每个小正方形的边长为1个单位,△ABC是格点三角形(顶点在网格交点处) .
(1)作出△ABC的中心对称图形△![]() ,A点为对称中心;
,A点为对称中心;
(2)作出△ABC关于点P的位似△A'B'C',且位似比为1:2;
(3)在图中画出以A、B、C为顶点的平行四边形的第四个顶点D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,扇形OAB的半径OA=4,圆心角∠AOB=90°,点C是弧AB上异于A、B的一点,过点C作CD⊥OA于点D,作CE⊥OB于点E,连结DE,过点C作弧AB所在圆的切线CG交OA的延长线于点G.
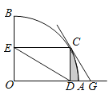
(1)求证:∠CGO=∠CDE;
(2)若∠CGD=60°,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了强化司机的交通安全意识,我市利用交通安全宣传月对司机进行了交通安全知识问卷调查.关于酒驾设计了如下调查问卷:
克服酒驾﹣﹣你认为哪种方式最好?(单选) |
A加大宣传力度,增强司机的守法意识. B在汽车上张贴温馨提示:“请勿酒驾”. C司机上岗前签“拒接酒驾”保证书. D加大检查力度,严厉打击酒驾. E查出酒驾追究一同就餐人的连带责任. |
随机抽取部分问卷,整理并制作了如下统计图:

根据上述信息,解答下列问题:
(1)本次调查的样本容量是多少?
(2)补全条形图,并计算B选项所对应扇形圆心角的度数;
(3)若我市有3000名司机参与本次活动,则支持D选项的司机大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
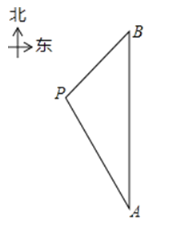
【题目】在一次海上救援中,两艘专业救助船![]() 同时收到某事故渔船的求救讯息,已知此时救助船
同时收到某事故渔船的求救讯息,已知此时救助船![]() 在
在![]() 的正北方向,事故渔船
的正北方向,事故渔船![]() 在救助船
在救助船![]() 的北偏西30°方向上,在救助船
的北偏西30°方向上,在救助船![]() 的西南方向上,且事故渔船
的西南方向上,且事故渔船![]() 与救助船
与救助船![]() 相距120海里.
相距120海里.
(1)求收到求救讯息时事故渔船![]() 与救助船
与救助船![]() 之间的距离;
之间的距离;
(2)若救助船A,![]() 分别以40海里/小时、30海里/小时的速度同时出发,匀速直线前往事故渔船
分别以40海里/小时、30海里/小时的速度同时出发,匀速直线前往事故渔船![]() 处搜救,试通过计算判断哪艘船先到达.
处搜救,试通过计算判断哪艘船先到达.
查看答案和解析>>
科目:初中数学 来源: 题型:
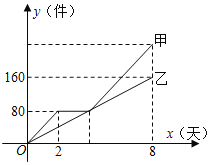
【题目】甲乙两个工厂同时加工一批机器零件.甲工厂先加工了两天后停止加工,维修设备,当维修完设备时,甲乙两厂加工的零件数相等,甲工厂再以原来的工作效率继续加工这批零件.甲乙两厂加工零件的数量y甲(件),y乙(件)与加工件的时间x(天)的函数图象如图所示,
(1)乙工厂每天加工零件的数为 件;
(2)甲工厂维修设备的时间是多少天?
(3)求甲维修设备后加工零件的数量y甲(件)与加工零件的时间x(天)的函数关系式,并写出自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E,F分别为BC,CD的中点,连接AE,BF交于点G,将△BCF沿BF对折,得到△BPF,延长FP交BA延长于点Q,下列结论正确的有( )个.
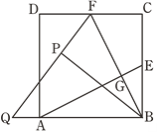
①AE⊥BF;②QB=QF;③![]() ;④SECPG=3S△BGE
;④SECPG=3S△BGE
A.1B.4C.3D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(概念认识)
若以三角形某边上任意一点为圆心,所作的半圆上的所有点都在该三角形的内部或边上,则将符合条件且半径最大的半圆称为该边关联的极限内半圆.
如图①,点P是锐角△ABC的边BC上一点,以P为圆心的半圆上的所有点都在△ABC的内部或边上.当半径最大时,半圆P为边BC关联的极限内半圆.
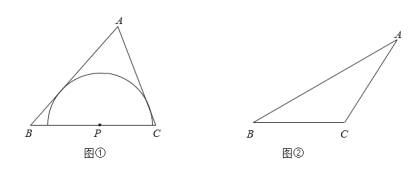
(初步思考)
(1)若等边△ABC的边长为1,则边BC关联的极限内半圆的半径长为 .
(2)如图②,在钝角△ABC中,用直尺和圆规作出边BC关联的极限内半圆(保留作图痕迹,不写作法).
(深入研究)
(3)如图③,∠AOB=30°,点C在射线OB上,OC=6,点Q是射线OA上一动点.在△QOC中,若边OC关联的极限内半圆的半径为r,当1≤r≤2时,求OQ的长的取值范围.
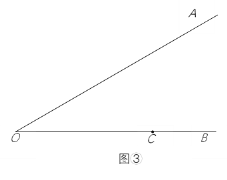
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com