
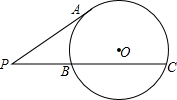
 以关于m的方程m2+(k-4)m+k=0的最大整数根为直径作⊙O.P为⊙O外一点,过P作切线PA和割线PBC,如图,A为切点.这时发现PA、PB、PC都是整数,且PB、BC都不是合数,求PA、PB、PC的长.
以关于m的方程m2+(k-4)m+k=0的最大整数根为直径作⊙O.P为⊙O外一点,过P作切线PA和割线PBC,如图,A为切点.这时发现PA、PB、PC都是整数,且PB、BC都不是合数,求PA、PB、PC的长.
|
|
|
|


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案科目:初中数学 来源: 题型:
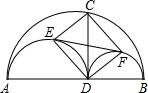 半圆,EF是这两个半圆的外公切线,E、F为切点.
半圆,EF是这两个半圆的外公切线,E、F为切点.查看答案和解析>>
科目:初中数学 来源: 题型:
| 4 | 3 |
 行四边形?若存在,请直接写出点M的坐标;若不存在,请说明理由.
行四边形?若存在,请直接写出点M的坐标;若不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
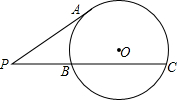 以关于m的方程m2+(k-4)m+k=0的最大整数根为直径作⊙O.P为⊙O外一点,过P作切线PA和割线PBC,如图,A为切点.这时发现PA、PB、PC都是整数,且PB、BC都不是合数,求PA、PB、PC的长.
以关于m的方程m2+(k-4)m+k=0的最大整数根为直径作⊙O.P为⊙O外一点,过P作切线PA和割线PBC,如图,A为切点.这时发现PA、PB、PC都是整数,且PB、BC都不是合数,求PA、PB、PC的长.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com