练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    15．已知AB⊥BC，AD⊥DC，且BC=DC，求证：∠ABD=∠ADB．

    分析 首先根据BC=CD得到∠CBD=∠CDB，再根据AB⊥BC，AD⊥DC得到∠ABC=∠ADC=90°，于是得到结论．

    解答 证明：∵BC=CD，
    ∴∠CBD=∠CDB，
    ∵AB⊥BC，AD⊥DC，
    ∴∠ABC=∠ADC=90°，
    ∴∠ABC-∠CBD=∠ADC-∠CDB，
    ∴∠ABD=∠ADB．

    点评 本题主要考查了等腰三角形的判定与性质，解题的关键是证明∠CBD=∠CDB，此题难度不大．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    14．最大的负整数是-1，绝对值最小的数是0，最小的正整数是1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    6．要把面值为10元一张的人民币换成零饯现有足够的面值为2元、1元的人民币，则有几种换法（　　）
    A．5种B．6种C．8种D．10种

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．解方程：
    （1）2x2+3=7x
    （2）x2-4x-3=0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

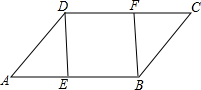    10．如图所示，已知AB=CD，AD=BC，DE=BF，且E，F分别是AB，CD的中点．
    （1）求证：∠A=∠C．
    （2）求证：∠EDF=∠FBE．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．解方程：
    ①x2-x-3=0                 
    ②2x（x-1）+3x-3=0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    7．（1）如图①，根据“SAS”，如果AB=AC，AD=AE，即可判定△ABD≌△ACE．
    （2）如图②，根据“SAS”，如果BD=CE，∠DBC=∠ECB，即可判定△BDC≌△CEB．
    （3）如图③，在△ABC中，AD=AE，BD=CE，∠ADB=∠AEC=105°，则△ABD≌△ACE．若∠B=40°，则∠CAE=45°．

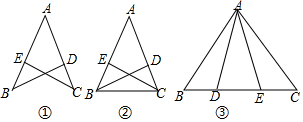
    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．解方程或不等式：
    （1）（3x-2）（2x-3）=（6x+5）（x-1）-1；
    （2）（3x+2）（3x-4）＞9（x-2）（x+3）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．某数学兴趣小组为了估计河的宽度，在河对岸选定一个8标点P，在近岸取点Q和S，使点P，Q，S共线且直找PS与河垂直，接着在过点S且与PS垂直的直线a上选择适当的点T，确定PT与过点Q且垂直PS的直线b的交点R．如果测得QS=45m，ST=90m，QS=60m，请计算河的宽度PQ．

    查看答案和解析>>

    同步练习册答案