
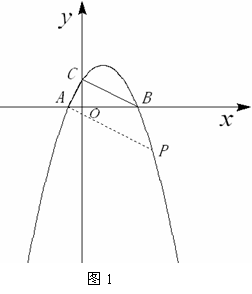
如图,二次函数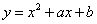 的图象与
的图象与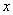 轴交于
轴交于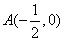 ,
,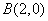 两点,且与
两点,且与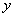 轴交于点
轴交于点 .
.
(1)求该抛物线的解析式,并判断 的形状;
的形状;
(2)在第一象限此抛物线上是否存在点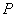 ,使得以
,使得以
四点为顶点的四边形是直角梯形?若存在,求出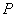 点的坐标;
点的坐标;
若不存在,说明理由.

解:根据题意,将A(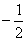 ,0),B(2,0)代入y=-x2+ax+b中,
,0),B(2,0)代入y=-x2+ax+b中,
得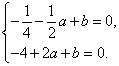
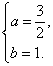 全所以抛物线的解析式为y=-x2+
全所以抛物线的解析式为y=-x2+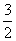 x+1.。。。。。(3分)
x+1.。。。。。(3分)
 当x=0时,y=1.所以点C的坐标为(0,1)。
当x=0时,y=1.所以点C的坐标为(0,1)。
所以在△AOC中,AC= =
=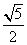 .
.
在△BOC中,BC=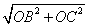 =
=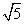 .
.
AB=OA+OB=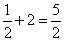 .
.
因为AC2+BC2=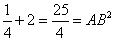 .
.
所以△ABC是直角三角形。  …………(6分)
…………(6分)
(2)存在。
由(1)知,AC⊥BC,
以BC为底边,则BC∥AP,如图(1 )所示,
)所示,
可求得直线BC的解析式为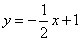 .
.
直线AP可以看作是由直线AC平移得到的,
所以设直线AP的解析式为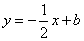 ,
,
将A(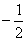 ,0)代入直线AP的解析式求得b=
,0)代入直线AP的解析式求得b=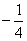 ,
,
所以直线AP的解析式为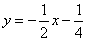 .
.
因为点P既在抛物线上,又在直线AP上,
所以点P的纵坐标相等 ,即-x2+
,即-x2+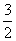 x+1=
x+1=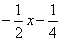 .
.
解得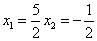 (不合题意,舍去).
(不合题意,舍去).
当x=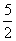 时,y=
时,y= .
.
所以点P的坐标为(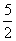 ,
, ).
).


科目:初中数学 来源: 题型:
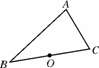
已知:如图23212,已知△ABC,点O为BC的中点.
(1)画出△ABC绕边BC的中点O旋转180°得到的△DCB;
(2)求证:四边形ABDC是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
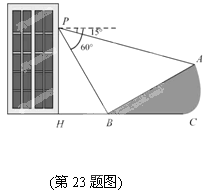
如图,小明在大楼30米高(即PH=30米,且PH⊥HC)的窗口P处进行 观测,测得山坡上A处的俯角为15
观测,测得山坡上A处的俯角为15 °,山脚B处得俯角为60°,已知该山坡的坡度
°,山脚B处得俯角为60°,已知该山坡的坡度 i(即tan∠ABC)为1:
i(即tan∠ABC)为1: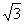 .(点P、H、B、C、A在同一个平面上.点H、B、C在同一条直线上)
.(点P、H、B、C、A在同一个平面上.点H、B、C在同一条直线上)
(1)山坡坡角(即∠ABC)的度数等于________度;(直接填空)
(2)求A、B两点间的距离(结果精确到0.1米,参考数据: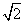 ≈1.414,
≈1.414,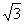 ≈1.732).
≈1.732).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com