
在平面直角坐标系xOy中,已知二次函数y1=ax2+3x+c的图像经过原点及点
A(1,2), 与x轴相交于另一点B.
(1)求:二次函数y1的解析式及B点坐标;
(2)若将抛物线y1以x=3为对称轴向右翻折后,得到一个新的二次函数y2,已知二次函数y2与x轴交于两点,其中右边的交点为C点. 点P在线段OC上,从O点出发向C点运动,过P点作x轴的垂线,交直线AO于D点,以PD为边在PD的右侧作正方形PDEF(当P点运动时,点D、点E、点F也随之运动);
①当点E在二次函数y1的图像上时,求OP的长.
②若点P从O点出发向C点做匀速运动,速度为每秒1个单位长度,同时线段OC上另一个点Q从C点出发向O点做匀速运动,速度为每秒2个单位长度(当Q点到达O点时停止运动,P点也同时停止运动).过Q点作x轴的垂线,与直线AC交于G点,以QG为边在QG的左侧作正方形QGMN(当Q点运动时,点G、点M、点N也随之运动),若P点运动t秒时,两个正方形分别有一条边恰好落在同一条直线上(正方形在x轴上的边除外),求此刻t的值.
【解】(1)∵二次函数y1=ax2+3x+c的图象经过原点及点A(1,2),
∴将(0,0),代入得出: c=0,
将(1,2)代入得出:a+3=2,解得:a=-1,
故二次函数解析式为:y1=-x2+3x,
∵图象与x轴相交于另一点B,
∴0=-x2+3x,
解得:x=0或3,
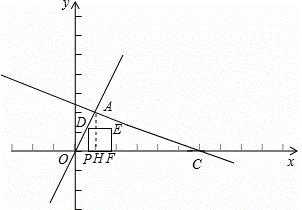 则B(3,0);(2)①由已知可得C(6,0)
则B(3,0);(2)①由已知可得C(6,0)
如图:过A点作AH⊥x轴于H点,设OP=m
∵DP∥AH,
∴△OPD∽△OHA,
∴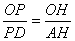 ,即
,即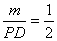 ,
,
∴PD=2m,∵正方形PDEF,
∴E(3m,2m),
∵E(3m,2m)在二次函数y1=-x2+3x的图象上,
∴m= ;
;
即OP= .
.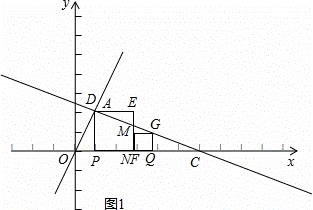 ②如图1:
②如图1:
当点F、点N重合时,有OF+CN=6,
∵直线AO过点(1,2),
故直线解析式为:y=2x,
当OP=t,
则AP=2t,
∵直线AC过点(1,2),(6,0),
代入y=kx+b,
 ,解得:
,解得: ,
,
故直线AC的解析式为:y=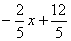 ,
,
∵当OP=t,QC=2t,
∴QO=6-2t,
∴GQ=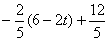 =
=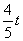
即NQ=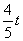 ,
,
 ∴OP+PN+NQ+QC=6,
∴OP+PN+NQ+QC=6,
则有3t+2t+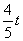 =6,
=6,
解得:t=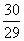 ;
;
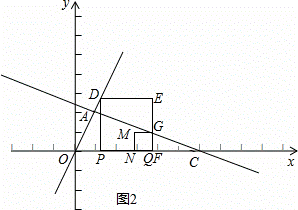
如图2:
当点F、点Q重合时,有OF+CQ=6,则有3t+2t=6,
解得:t=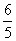 ;
;
如图3:
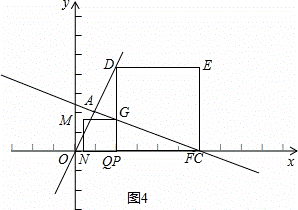 当点P、点N重合时,有OP+CN=6,则有t+2t+
当点P、点N重合时,有OP+CN=6,则有t+2t+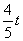 =6,
=6,
解得:t= ,
,
如图4:
当点P、点Q重合时,有OP+CQ=6,则有t+2t=6,
解得:t=2.
故此刻t的值为:t1=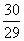 ,t2=
,t2=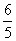 ,t3=
,t3= ,t4=2.
,t4=2.


科目:初中数学 来源: 题型:
图中给出的直线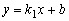 和反比例函数
和反比例函数 的图像,判断下列结论正确的有( )
的图像,判断下列结论正确的有( )
①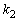 >
>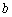 >
> >0; ②直线
>0; ②直线 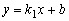 与坐标轴围成的△ABO的面积是4;
与坐标轴围成的△ABO的面积是4;
③方程组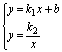 的解为
的解为 ,
,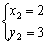 ; ④当-6<x<2时,有
; ④当-6<x<2时,有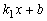 >
>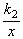 .
.
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
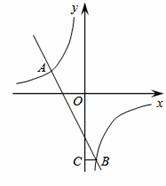
如图,在平面直角坐标系中,双曲线 和直线y=kx+b交于A,B两点,点A的坐标为(﹣3,2),BC⊥y轴于点C,且OC=6BC.
和直线y=kx+b交于A,B两点,点A的坐标为(﹣3,2),BC⊥y轴于点C,且OC=6BC.
(1)求双曲线和直线的解析式;
(2)直接写出不等式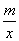 >
>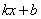 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
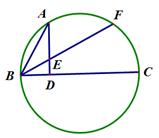
如图,BC是圆的直径,AD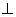 BC,垂足为点D,弧BA=弧AF,BF与AD交于点E。
BC,垂足为点D,弧BA=弧AF,BF与AD交于点E。
求证:AE=BE;
若点A. F 把半圆三等分,BC=12,求AE的长。
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
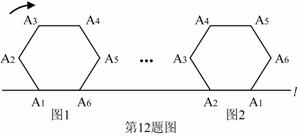
如图,将边长为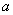 的正六边形A1 A2 A3 A4 A5 A6在直线
的正六边形A1 A2 A3 A4 A5 A6在直线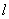 上由图1的位置按顺时针方
上由图1的位置按顺时针方
向向右作无滑动滚动,当A1第一次滚动到图2位置时,顶点A1所经过的路径的
长为( ).
A. 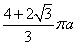 B.
B. 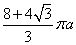 C.
C. 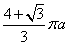 D.
D. 
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
如图6,一次函数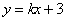 的图象分别交x轴、y轴于点C、点D,与反比例函数
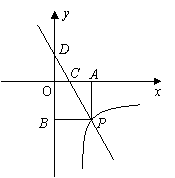
的图象分别交x轴、y轴于点C、点D,与反比例函数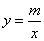 的图象在第四象限的相交于点P,并且PA⊥x轴于点A,PB⊥y轴于点B,已知B(0,-6), 且S△DBP=27
的图象在第四象限的相交于点P,并且PA⊥x轴于点A,PB⊥y轴于点B,已知B(0,-6), 且S△DBP=27
(1)求上述一次函数与反比例函数的表达式;
(2)求一次函数与反比例函数的另一个交点坐标。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com