
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
| 序号 | 1 | 2 | 3 | … |
图形 | x x y x x y x x | x x x y y x x x y y x x x | x x x x y y y x x x x y y y x x x x | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
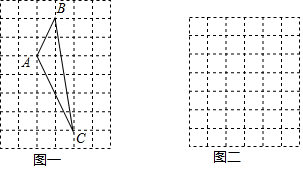
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
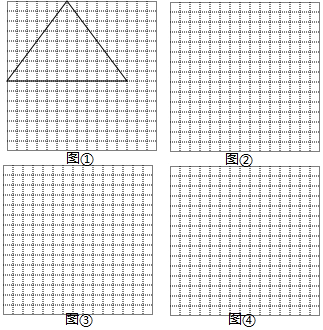 如图,在15×15的网格中,每个小正方形的边长均为1,每个小格的顶点叫做格点,图①中的三角形是以格点为顶点,边长都为整数的锐角三角形.
如图,在15×15的网格中,每个小正方形的边长均为1,每个小格的顶点叫做格点,图①中的三角形是以格点为顶点,边长都为整数的锐角三角形.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
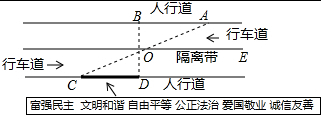 小明沿一段笔直的人行道行走,在由A步行到达B处的过程中,通过隔离带的空隙0点,刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语,其具体信息如下:如图,AB∥OE,OE∥CD,AC与BD相交于点O,OD⊥CD,垂足为点D,下列结论中不正确的是( )
小明沿一段笔直的人行道行走,在由A步行到达B处的过程中,通过隔离带的空隙0点,刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语,其具体信息如下:如图,AB∥OE,OE∥CD,AC与BD相交于点O,OD⊥CD,垂足为点D,下列结论中不正确的是( )| A. | ∠BOA=∠DOC | B. | AB∥CD | ||
| C. | ∠ABD=90° | D. | 与∠AOE相等的角共有2个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
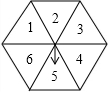 如图所示的是一个正六边形转盘被分成6个全等的等边三角形,指针位置固定,转动转盘后任其自由停止,其中的某个三角形会恰好停在指针所指的位置,并相应得到一个数 (指针指向两个三角形的公共边时,当作指向右边的三角形),这时称转动了转盘1次.
如图所示的是一个正六边形转盘被分成6个全等的等边三角形,指针位置固定,转动转盘后任其自由停止,其中的某个三角形会恰好停在指针所指的位置,并相应得到一个数 (指针指向两个三角形的公共边时,当作指向右边的三角形),这时称转动了转盘1次.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com