
【题目】生活中,有人喜欢把传送的便条折成“![]() ”形状,折叠过程按图①、②、③、④的顺序进行(其中阴影部分表示纸条的反面):
”形状,折叠过程按图①、②、③、④的顺序进行(其中阴影部分表示纸条的反面):
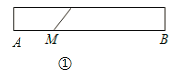

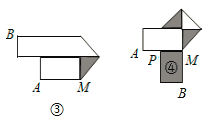
如果由信纸折成的长方形纸条(图①)长为2 6 厘米,分别回答下列问题:
(1)如果长方形纸条的宽为2厘米,并且开始折叠时起点M与点A的距离为3厘米,那么在图②中,BE=_____厘米; 在图④中,BM=______厘米.
(2)如果长方形纸条的宽为x厘米,现不但要折成图④的形状,而且为了美观,希望纸条两端超出点P的长度相等,即最终图形是轴对称图形,试求在开始折叠时起点M与点A的距离(结果用x表示).
 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
【题目】探索规律:观察下面由※组成的图案和算式,解答问题:

1+3=22=4
1+3+5=32=9
1+3+5+7=42=16
1+3+5+7+9=52=25
(1)猜想1+3+5+7+9+…+29= = ;
(2)猜想1+3+5+7+9+…+(2n﹣1)+(2n+1)= = ;
(3)用上述规律计算:41+43+45+…+77+79.
查看答案和解析>>
科目:初中数学 来源: 题型:
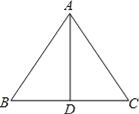
【题目】如图,AD是△ABC的边BC上的高,由下列条件中的某一个就能推出△ABC是等腰三角形的是__.
①∠BAD=∠ACD;②∠BAD=∠CAD;③AB+BD=AC+CD;④AB﹣BD=AC﹣CD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】雷达二维平面定位的主要原理是:测量目标的两个信息―距离和角度,目标的表示方法为![]() ,其中,m表示目标与探测器的距离;
,其中,m表示目标与探测器的距离;![]() 表示以正东为始边,逆时针旋转后的角度.如图,雷达探测器显示在点A,B,C处有目标出现,其中,目标A的位置表示为
表示以正东为始边,逆时针旋转后的角度.如图,雷达探测器显示在点A,B,C处有目标出现,其中,目标A的位置表示为![]() ,目标C的位置表示为
,目标C的位置表示为![]() .用这种方法表示目标B的位置,正确的是( )
.用这种方法表示目标B的位置,正确的是( )

A. (-4, 150°) B. (4, 150°) C. (-2, 150°) D. (2, 150°)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com