
����Ŀ���ڡ�ABC�У�AB��BC��2![]() ����ABC��120�㣬��CDEΪ�ȱ������Σ�CD��2������AD��MΪAD�е㣮
����ABC��120�㣬��CDEΪ�ȱ������Σ�CD��2������AD��MΪAD�е㣮
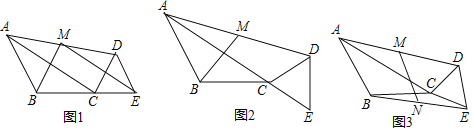
��1����ͼ1����B��C��E���㹲��ʱ���뻭����EDM���ڵ�M�����ĶԳ�ͼ�Σ���֤��BM��ME��
��2����ͼ2����A��C��E���㹲��ʱ����BM�ij���
��3����ͼ3��ȡBE�е�N����MN������CDE�Ƶ�C��ת��ֱ��д����ת�������߶�MN��ȡֵ��Χ��_____��
���𰸡���1���𰸼���������2��![]() ����3��
����3��![]() ��
��
��������
��1��������ͼ�Σ�����֤����AMF�ա�DME�����ɵó����ۣ�
��2��ͬ��1���ķ����ó���AMF�ա�DMF�������ı��ε��ڽǺͶ�����ƽ�ǵĶ���ó���BCE����BAF���ɵó���BME��90�㣬����ù��ɶ������ɵó����ۣ�
��3��ͬ��2���ķ����ó���BME��90�㣬�����ó�BE��2MN������������ε����߹�ϵ���ɵó����ۣ�
�⣺��1��֤������ͼ1��
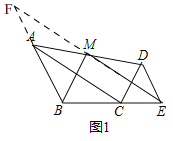
�ӳ�BA��EM���ڵ�F��������FAM��Ϊ����
�ߡ�CDE�ǵȱ������Σ�
��CD��CE��DE����CED��60�㣬
�ߡ�ABC��120�㣬
���ABC+��CED��180�㣬
��B��C��E���㹲�ߣ�
��AB��DE��
���FAM����MDE����MED����F��
�ߵ�M��AD�е㣬
��AM��DM��
���AMF�ա�DME��
��AF��DE��CE��FM��ME��
��AB��BC��
��BF��BE��
��BM��ME��
��2��֤������ͼ2���ӳ�EM����F��ʹMF��ME������BF��AF��BE��
��AM��DM����FMA����DME��
���AMF�ա�DMF��
��AF��DE��CE����FAD����ADE��
���ı���BADE�У��ߡ�BAD+��ADE+��DEB+��EBA��360�㣬
�ߡ�ABC��120�㣬��CED��60�㣬
���CBE+��CEB+��BAD+��ADE��180�㣬
�ߡ�CBE+��CEB+��BCE��180�㣬
���BCE����BAD+��ADE��
���BCE����BAF��
��AB��AC��
���AFB�ա�CEB��
��BF��BE����ABF����CBE��
���FBE����ABC��120�㣬��BEF��30�㣬
���BME��90�㣬BE��2BM��
�ڡ�ABC�У�AB��AC��2![]() ����ABC��120�㣬���BAC��30�㣬
����ABC��120�㣬���BAC��30�㣬
����B��BG��AC��G��
��BG��![]() ��CG��AG��3��
��CG��AG��3��
��EG��CG+CE��3+2��5
��Rt��BCE�У����ݹ��ɶ����ã�BE��2![]() ��
��
��BM��![]() ��
��
��3����ͼ3���ӳ�EM����F��ʹMF��ME������BF��AF��BM��
��AM��DM����FMA����DME��
���AMF�ա�DME��
��AF��DE��CE����FAD����ADE��
���ı���BADE�У��ߡ�BAD+��ADE+��DEB+��EBA��360�㣬
�ߡ�ABC��120�㣬��CED��60�㣬
���CBE+��CEB+��BAD+��ADE��180�㣬
�ߡ�CBE+��CEB+��BCE��180�㣬
���BCE����BAD+��ADE��
���BCE����BAF��
��AB��CB��
���AFB�ա�CEB��
��BF��BE����ABF����CBE��
���FBE����ABC��120�㣬��BEF��30�㣬
���BME��90�㣬
�ߵ�N��BE���е㣬
��MN��![]() BE��
BE��
����BE��2MN��
�ڡ�BCE�У�BC��2![]() ��CE��CD��2��
��CE��CD��2��
��2![]() ��2��BE��2
��2��BE��2![]() +2��
+2��
��2![]() ��2��2MN��2
��2��2MN��2![]() +2��
+2��
����![]() ��1��MN��
��1��MN��![]() +1��
+1��
�ʴ�Ϊ��![]() ��1��MN��
��1��MN��![]() +1��
+1��





| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�ȱ���ABC����DΪBC��һ�㣬����AD.

ͼ1 ͼ2
��1������E��AC��һ�㣬��CE��BD������BE��BE��AD�Ľ���Ϊ��P����ͼ��1���и������ⲹȫͼ�Σ�ֱ��д����APE�Ĵ�С��
��2����AD�Ƶ�A��ʱ����ת120�����õ�AF������BF��AC�ڵ�Q����ͼ��2���и������ⲹȫͼ�Σ��õ�ʽ��ʾ�߶�AQ��CD��������ϵ����֤��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������ڰ�װ��������ͼ��ʾ����A������ת����֧�㣬��E���������ε�����㣮����������ʱ������AEF���ֻ��������ͼ2��ʾ��λ�ã���ʾ��ͼ��ͼ3��ʾ�����˿��Ⱥ��Բ��ƣ�������AB��BC��EF��BC����AEF��143�㣬AB��1.18�ף�AE��1.2�ף���ô�ʺϸõ��³���ij����߱�־��Ϊ�����������ο����ݣ�sin37���0.60��cos37���0.80��tan37���0.75��
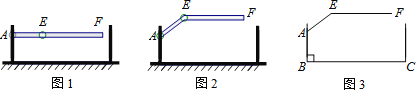
A. B.
B. C.
C. D.
D.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������У�ٰ�ġ������顢�����ǡ���У���������ж���ͼ��ǵ����顢���鲻�����࣬��ѧУ�����ͼ���⣬����ʦ������ͼ�飬�����Ǿţ�1����ȫ��ͬѧ����ͼ�������ͳ��ͼ��ÿ�˶��о�������
�����������ͳ��ͼ�е���Ϣ������������⣺
��1���ð���ѧ�������ˣ�
��2����ȫ����ͳ��ͼ��
��3���ţ�1����ȫ��ͬѧ����ͼ���� 6 ��������������ͳ��ͼ������Ӧ���ε�Բ�Ľ�Ϊ���ٶȣ�
��4���������ȫУ 2000 ��ѧ������ͼ���������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ,AB��6,AC��3,��BAC��60��,![]() Ϊ��O�ϵ�һ�λ�,�ҡ�BOC��60��,�ֱ���
Ϊ��O�ϵ�һ�λ�,�ҡ�BOC��60��,�ֱ���![]() ���߶�AB��AC��ѡȡ��P��E��F,��PE��EF��FP����СֵΪ__________
���߶�AB��AC��ѡȡ��P��E��F,��PE��EF��FP����СֵΪ__________

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ʒ�Ľ���Ϊÿ��10Ԫ�����ڵ��ۼ�Ϊÿ��15Ԫ��ÿ�ܿ�����100�����г����鷴ӳ�����ÿ�����ۼ�ÿ��1Ԫ���ۼ�ÿ�����ܸ���20Ԫ������ôÿ������10��.��ÿ���Ǽ�![]() Ԫ��
Ԫ��![]() Ϊ�Ǹ���������ÿ�ܵ�����Ϊ
Ϊ�Ǹ���������ÿ�ܵ�����Ϊ![]() ��.
��.
��1����![]() ��
��![]() �ĺ�����ϵʽ���Ա���
�ĺ�����ϵʽ���Ա���![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2�������Ӫ����Ʒÿ�ܵ�������560Ԫ����ÿ����Ʒ���ۼ��Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����в��ϣ��������Ӧ������.

����
��1������֤�������еġ�����1���͡�����2���ֱ�ָʲô��
����1��
����2��
��2����Բ�ڽ��ı���ABCD�Ǿ���ʱ�������ܶ����������Ƿdz���֪��һ�������� ����д���������ƣ�.
��3����ͼ��3�����ı���ABCD�ڽ�����O��AB=3��AD=5����BAD=60�㣬��C�ǻ�BD���е㣬��AC�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�½���վվǰ�㳡��Ҫ�̻������Ϊ46000��2��ʩ�������̻���22000��2��ÿ��Ĺ���������Ϊԭ����1.5���������ǰ4������˸����̻����̣�
��1�������̻�����ԭ�ƻ�ÿ����ɶ�����2��
��2�������̻���������һ�鳤Ϊ20�ף���Ϊ8�ľ��οյأ��ƻ���������������ͬ�ľ����̵أ����ǵ����֮��Ϊ56��2�������̵�֮�估�ܱ����п�����ȵ�����ͨ������ͼ��ʾ����������ͨ���Ŀ����Ƕ����ף�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�����AOB��ͼ����1��������OA��ȡһ��C���Ե�OΪԲ�ģ�OC��Ϊ�뾶��![]() ��������OB�ڵ�D������CD��
��������OB�ڵ�D������CD��
��2���ֱ��Ե�C��DΪԲ�ģ�CD��Ϊ�뾶��������![]() �ڵ�M��N��
�ڵ�M��N��
��3������OM��MN��
����������ͼ���̼�����ͼ�Σ����н����д�����ǣ� ��

A. ��COM=��CODB. ��OM=MN������AOB=20��
C. MN��CDD. MN=3CD
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com