
【题目】如图,△ABC为等腰三角形,AC=BC,△BDC和△ACE分别为等边三角形,直线AE与BD相交于点F,连接CF,交AB于点G.
(1)若∠ACB=150°,求∠AFB的度数;
(2)求证:AG=BG.
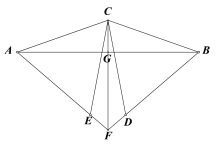
【答案】(1)90°;(2)详见解析.
【解析】
(1)由△BDC和△ACE分别为等边三角形可知∠CAF=∠CBD=60°,再由四边形的内角和为360°可求解∠AFB的度数;
(2)由AC=BC可得∠CAB=∠CBA,再由∠CAF=∠CBD=60°可得∠BAF=∠ABF,则AF=BF,据此易证△CAF≌△CBF得∠ACG=∠BCG,则可证明△ACG≌△BCG从而得到AG=BG.
(1)解:∵△BDC和△ACE分别为等边三角形,
∴∠CAF=∠CBD=60°,
∴∠AFB=360°-∠ACB-∠CAF-∠CBD=360°-150°-60°-60°=90°;
(2)证明:∵AC=BC,
∴∠CAB=∠CBA,
∵△BDC和△ACE分别为等边三角形,
∴∠CAF=∠CBD=60°,
∴∠BAF=∠CAF-∠CAB=∠CBD-∠CBA=∠ABF,
∴AF=BF,
∵AC=BC,∠CAF=∠CBD=60°,AF=BF,
∴△CAF≌△CBF,
∴∠ACG=∠BCG,
又∵AC=BC,∠CAB=∠CBA,
∴△ACG≌△BCG,
∴AG=BG.


科目:初中数学 来源: 题型:
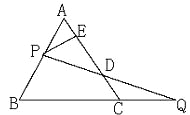
【题目】如图,过边长为1的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,当PA=CQ时,连PQ交AC边于D,则DE的长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 不能确定
D. 不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
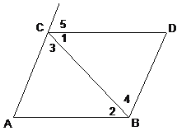
【题目】如图,完成下列推理过程,已知AB∥CD,AC∥BD,
(1)∵AB∥CD(已知) ∴∠A=∠5(两直线平行,_______________);
(2)∵AC∥BD(已知) ∴∠3=∠4(两直线平行,_______________);
(3)∵AB∥CD(已知) ∴∠__=∠___(两直线平行,內錯角相等);
(4)∵AB∥CD(已知) ∴∠D +∠______ =180°(两直线平行,____)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】保护环境、低碳出行已渐渐成为人们的习惯.最近无为县城又引进了共享单车,只需要交点押金,就可以通过扫描二维码的方式解锁一辆停在路边的自行车,以极低的费用,轻松骑到目的地.王老师家与学校相距2km,现在每天骑共享单车到学校所花的时间比过去骑电动车多用4min.已知王老师骑电动车的速度是骑共享单车速度的1.5倍,则王老师骑共享单车的速度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学广场上有旗杆,在学习解直角三角形以后,数学兴趣小组测量了旗杆的高度.如图2,某一时刻,旗杆AB的影子一部分落在平台上,另一部分落在斜坡上,测得落在平台上的影长BC为4米,落在斜坡上的影长CD为3米,AB⊥BC,同一时刻,光线与水平面的夹角为72°,1米的竖立标杆PQ在斜坡上的影长QR为2米,求旗杆的高度(结果精确到0.1米).(参考数据:sin72°≈0.95,cos72°≈0.31,tan72°≈3.08) 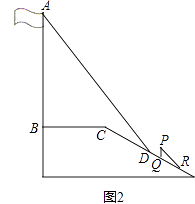
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实验探究题
(1)操作发现:
在△ABC中,AB=AC,∠BAC=90°,D在线段BC上(不与点B重合),连接AD,将线段AD绕A点逆时针旋转90°得到AE,连接EC,如图①所示,请直接写出线段CE和BD的位置关系和数量关系.
(2)猜想论证:
在(1)的条件下,当D在线段BC的延长线上时,请你在图②中画出图形并判断(1)中的结论是否成立,并证明你的判断.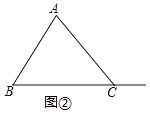
(3)拓展延伸:
如图③,若AB≠AC,∠BAC≠90°,点D在线段BC上运动,试探究:当锐角∠ACB等于度时,线段CE和BD之间的位置关系仍成立(点C、E重合除外)?此时若作DF⊥AD交线段CE于点F,且当AC=3 ![]() 时,请直接写出线段CF的长的最大值是 .
时,请直接写出线段CF的长的最大值是 . 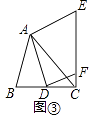
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,半径为2的正六边形ABCDEF的中心在坐标原点O,点P从点B出发,沿正六边形的边按顺时针方向以每秒2个单位长度的速度运动,则第2017秒时,点P的坐标是( ) 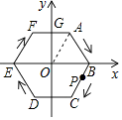
A.(1, ![]() )
)
B.(﹣1,﹣ ![]() )
)
C.(1,﹣ ![]() )
)
D.(﹣1, ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
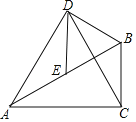
【题目】如图,在Rt△ABC中,(M2,N2),∠BAC=30°,E为AB边的中点,以BE为边作等边△BDE,连接AD,CD.
(1)求证:△ADE≌△CDB;
(2)若BC=![]() ,在AC边上找一点H,使得BH+EH最小,并求出这个最小值.
,在AC边上找一点H,使得BH+EH最小,并求出这个最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
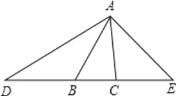
【题目】如图,在△ABC 中,∠ABC=50°,∠ACB=80°,延长 CB 至 D,使 DB=BA,延长 BC 至 E,使 CE=CA,连接 AD 和 AE,求∠D,∠DAE 的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com