
分析 利用反例对①②进行判断;利用平方差公式得到(a+c)2-b2<0,则b2-4ac>(a-c)2,然后根据根的判别式的意义可对③进行判断;由于b2+4ac<0,而b2≥0,则4ac<0,所以b2-4ac>0,然后根据根的判别式的意义可对④进行判断;先由ac<0判断方程一定有两个不相等的实数根,然后根据根与系数的关系对⑤进行判断.
解答 解:若c是一元二次方程ax2+bx+c=0的一个根,当c=0时,则不一定有ac+b+1=0,所以①错误;
当a=-1,b=0,c=0时,一元二次方程ax2+bx+c=0有两个相等的实数根,所以②错误;
若a+b+c>0,a-b+c<0,则(a+c+b)(a+c-b)<0,(a+c)2-b2<0,b2-4ac>(a-c)2,所以b2-4ac>0,则方程ax2+bx+c=0一定有两个不相等的实数根,所以③正确;
因为b2+4ac<0,而b2≥0,则4ac<0,所以b2-4ac>0,所以方程ax2+bx+c=0有两个不相等的实数根,所以④正确;
因为ac<0,则b2-4ac>0,所以方程一定有两个不相等的实数根,而b=0,方程两根之和为0,所以方程两个实数根一定互为相反数,所以⑤正确.
故答案为3..
点评 本题考查了命题与定理:判断一件事情的语句,叫做命题.许多命题都是由题设和结论两部分组成,题设是已知事项,结论是由已知事项推出的事项,一个命题可以写成“如果…那么…”形式. 有些命题的正确性是用推理证实的,这样的真命题叫做定理.要说明一个命题的正确性,一般需要推理、论证,而判断一个命题是假命题,只需举出一个反例即可.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:解答题
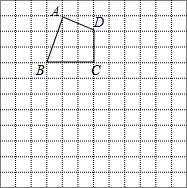 作图题:(不要求写作法)如图,在10×10的方格纸中,有一个格点四边形ABCD(即四边形的顶点都在格点上)
作图题:(不要求写作法)如图,在10×10的方格纸中,有一个格点四边形ABCD(即四边形的顶点都在格点上)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,矩形ABCD中,AB=7,AD=5,点E在CD上,把△ADE沿AE折叠,当点D的对应点D′落在∠ABC的平分线上时,点D′到AB的距离是3或4.
如图,矩形ABCD中,AB=7,AD=5,点E在CD上,把△ADE沿AE折叠,当点D的对应点D′落在∠ABC的平分线上时,点D′到AB的距离是3或4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
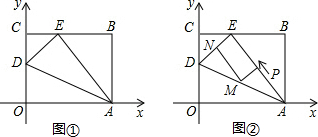
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com