
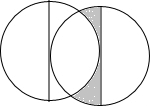
 半径为1的两圆放置位置如图所示,一圆的直径恰好是另一圆的切线,圆心均为切点,则阴影部分的面积为$\frac{\sqrt{3}}{2}$-$\frac{π}{6}$.
半径为1的两圆放置位置如图所示,一圆的直径恰好是另一圆的切线,圆心均为切点,则阴影部分的面积为$\frac{\sqrt{3}}{2}$-$\frac{π}{6}$. 分析 如图,连接AO1,BO1,AO2,BO2,O1O2,AB,于是得到四边形AO1BO2是菱形,△AO1O2是等边三角形,求得∠O1AO2=60°,∠AO1B=120°,根据扇形和三角形的面积公式即可得到结论.
解答 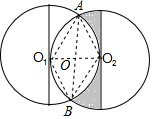 解:如图,连接AO1,BO1,AO2,BO2,O1O2,AB,
解:如图,连接AO1,BO1,AO2,BO2,O1O2,AB,
则四边形AO1BO2是菱形,△AO1O2是等边三角形,
∴∠O1AO2=60°,∠AO1B=120°,
∴S${\;}_{弓形A{O}_{1}B}$=S${\;}_{扇形A{O}_{2}B}$-S${\;}_{△AB{O}_{2}}$=$\frac{120•π×{1}^{2}}{360}$-$\frac{1}{2}$×$\sqrt{3}$×$\frac{1}{2}$=$\frac{π}{3}$-$\frac{\sqrt{3}}{4}$,
∴阴影部分的面积=S半圆-2S${\;}_{弓形A{O}_{1}B}$=$\frac{π}{2}$-2($\frac{π}{3}$-$\frac{\sqrt{3}}{4}$)=$\frac{\sqrt{3}}{2}$-$\frac{π}{6}$;
故答案为:$\frac{\sqrt{3}}{2}$-$\frac{π}{6}$;
点评 本题考查了扇形的面积的计算,菱形的判定和性质,正确的作出辅助线是解题的关键.


科目:初中数学 来源: 题型:填空题
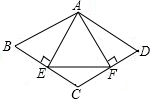 如图,平行四边形ABCD中,AE⊥BC,AF⊥CD,垂足分别为E,F,连结EF,给出下列判断:①若△AEF是等边三角形,则∠B=60°,②若∠B=60°,则△AEF是等边三角形,③若AE=AF,则平行四边形ABCD是菱形,④若平行四边形ABCD是菱形,则AE=AF,其中,结论正确的是①③④(只需填写正确结论的序号).
如图,平行四边形ABCD中,AE⊥BC,AF⊥CD,垂足分别为E,F,连结EF,给出下列判断:①若△AEF是等边三角形,则∠B=60°,②若∠B=60°,则△AEF是等边三角形,③若AE=AF,则平行四边形ABCD是菱形,④若平行四边形ABCD是菱形,则AE=AF,其中,结论正确的是①③④(只需填写正确结论的序号).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
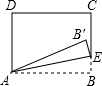 如图,矩形ABCD中,点E为射线BC上的一个动点,连接AE,以AE为对称轴折叠△AEB,得到△AEB′,点B的对称点为点B′,若AB=5,BC=3,当点B′落在射线CD上时,线段BE的长为$\frac{5}{3}$或15.
如图,矩形ABCD中,点E为射线BC上的一个动点,连接AE,以AE为对称轴折叠△AEB,得到△AEB′,点B的对称点为点B′,若AB=5,BC=3,当点B′落在射线CD上时,线段BE的长为$\frac{5}{3}$或15.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
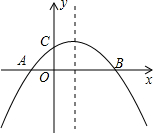 如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C,且OA=OC.则下列结论:①abc<0;②$\frac{{b}^{2}-4ac}{4a}$>0;③ac-b+1=0;④2a+b=0其中正确结论的个数是( )
如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C,且OA=OC.则下列结论:①abc<0;②$\frac{{b}^{2}-4ac}{4a}$>0;③ac-b+1=0;④2a+b=0其中正确结论的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
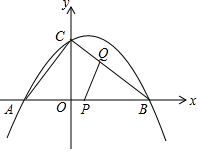 综合与探究:如图,抛物线y=ax2+bx+$\frac{12}{5}$与x轴交于A(-$\frac{9}{5}$,0),B($\frac{16}{5}$,0)两点,与y轴交于点C,连接AC,BC,一动点P从点A出发,沿线段AB向终点B以每秒1个单位长度的速度运动;同时,点Q从点B出发,以相同的速度沿线段BC向终点C运动,当其中一个动点到达终点时,另一个动点也随之停止运动,连接PQ.设P,Q两点运动时间为t秒.
综合与探究:如图,抛物线y=ax2+bx+$\frac{12}{5}$与x轴交于A(-$\frac{9}{5}$,0),B($\frac{16}{5}$,0)两点,与y轴交于点C,连接AC,BC,一动点P从点A出发,沿线段AB向终点B以每秒1个单位长度的速度运动;同时,点Q从点B出发,以相同的速度沿线段BC向终点C运动,当其中一个动点到达终点时,另一个动点也随之停止运动,连接PQ.设P,Q两点运动时间为t秒.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com