
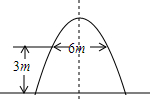
 蔬菜大棚的支架是抛物线型,跨度是8m,内侧距离地面高度相等处各有一螺栓,螺栓之间的水平距离为6m,请建立适当的直角坐标系,写出这段抛物线所对应的二次函数的表达式,并求出支架最高点距地面的距离(精确到0.1m)
蔬菜大棚的支架是抛物线型,跨度是8m,内侧距离地面高度相等处各有一螺栓,螺栓之间的水平距离为6m,请建立适当的直角坐标系,写出这段抛物线所对应的二次函数的表达式,并求出支架最高点距地面的距离(精确到0.1m) 分析 根据题意,以跨度的中点为坐标原点,地面为x轴,建立平面直角坐标系,抛物线的解析式为y=ax2+k,并且过(4,0),(3,3),利用待定系数法求它的表达式则可;进一步代入x=0,得出最大值即可.
解答 解:如图,
以跨度的中点为坐标原点,地面为x轴,建立平面直角坐标系,
设抛物线的解析式为y=ax2+k,代入点(4,0),(3,3)得
$\left\{\begin{array}{l}{16a+k=0}\\{9a+k=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-\frac{3}{7}}\\{k=\frac{48}{7}}\end{array}\right.$
因此抛物线的解析式为y=-$\frac{3}{7}$x2+$\frac{48}{7}$.
当x=0时,y最大为$\frac{48}{7}$≈6.9米,
即支架最高点距地面的距离为6.9米.
点评 此题考查二次函数的实际运用,待定系数法求函数解析式,建立适当的坐标系,得出点的坐标是解决问题的关键.


科目:初中数学 来源: 题型:解答题
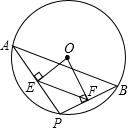 如图,AB是⊙O的弦,点P是⊙O上的动点(P与A、B不重合)连接AP,BP,过点O分别作OE⊥AP于点E,OF⊥PB于点F,试猜想在运动过程中,EF与AB具有怎样的关系,并说明理由.
如图,AB是⊙O的弦,点P是⊙O上的动点(P与A、B不重合)连接AP,BP,过点O分别作OE⊥AP于点E,OF⊥PB于点F,试猜想在运动过程中,EF与AB具有怎样的关系,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
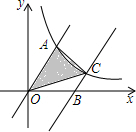 如图,直线y=2x与双曲线y=$\frac{k}{x}$(x>0)相交于点A,过点B(3,0)作直线BC∥0A,交该双曲线于点C,若△0AC的面积是3$\sqrt{3}$,则k的值是6.
如图,直线y=2x与双曲线y=$\frac{k}{x}$(x>0)相交于点A,过点B(3,0)作直线BC∥0A,交该双曲线于点C,若△0AC的面积是3$\sqrt{3}$,则k的值是6.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $({-\frac{2}{3}})$和$-\frac{2}{3}$ | B. | $({-\frac{2}{3}})$和$-\frac{3}{2}$ | C. | $({-\frac{2}{3}})$和$\frac{2}{3}$ | D. | $({-\frac{2}{3}})$和$\frac{3}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com