
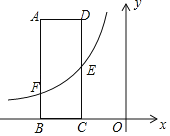
【题目】如图,矩形ABCD的两边AD、AB的长分别为3、8,E是DC的中点,反比例函数y=![]() 的图象经过点E,与AB交于点F.
的图象经过点E,与AB交于点F.
(1)若点B坐标为(﹣6,0),求图象经过A、E两点的一次函数的表达式是_____;
(2)若AF﹣AE=2,则反比例函数的表达式是_____.
【答案】(1)y=﹣![]() x;(2)y=﹣
x;(2)y=﹣![]() .
.
【解析】
(1)作直线AE,利用矩形的性质得到A(﹣6,8),C(﹣3,0),D(﹣3,8),从而求出点E的坐标,然后利用待定系数法即可求出直线AE的表达式;
(2)利用勾股定理计算出AE,从而求出AF,设B(t,0),则F(t,1),C(t+3,0),E(t+3,4),利用反比例函数图象上点的坐标特征即可求出t的值,然后计算出m的值,从而得到此时反比例函数的表达式.
解:(1)作直线AE
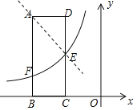
∵矩形ABCD的两边AD、AB的长分别为3、8,若点B坐标为(﹣6,0),
∴A(﹣6,8),C(﹣3,0),D(﹣3,8),
∵E是DC的中点,
∴E(﹣3,4),
设直线AE的解析式为y=kx+b,
把A(﹣6,8),E(﹣3,4)代入得![]() ,
,
解得 ,
,
∴图象经过A、E两点的一次函数的表达式为y=﹣![]() x
x
故答案为y=﹣![]() x;
x;
(2)∵AE=![]() =
=![]() =5,
=5,
而AF﹣AE=2,
∴AF=7,
设B(t,0),则F(t,1),C(t+3,0),E(t+3,4),
∵F(t,1),E(t+3,4)在反比例函数y=![]() 的图象上,
的图象上,
∴t×1=4(t+3),
解得t=﹣4,
∴F(﹣4,1),
∴m=﹣4×1=﹣4,
∴若AF﹣AE=2,则反比例函数的表达式是y=﹣![]() .
.
故答案为y=﹣![]() .
.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:
【题目】小红参加学校组织的庆祝党的十九大胜利召开知识竞赛,答对最后两道单选题就顺利通关,第一道单选题有3个选项,第二道单选题有4个选项,可是小红这两道题都不会,不过竞赛规则规定每位选手有两次求助机会,使用“求助”一次可以让主持人去掉其中一题的一个错误选项,主持人提醒小红可以使用两次“求助”.
(1)如果小红两次“求助”都在第一道题中使用,那么小红通关的概率是 .
(2)如果小红将每道题各用一次“求助”,请用树状图或者列表来分析她顺序通关的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
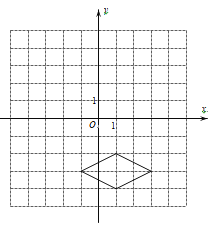
【题目】在平面直角坐标系中,x轴下方有一个菱形,如图所示,画图并回答问题.
(1)将x轴下方的菱形先向右平移2个单位长度,再向上平移6个单位长度,画出平移后的图形;
(2)将x轴下方的菱形绕着原点顺时针方向旋转 90°,画出旋转后的图形;
(3)在(1)和(2)中画出的两个图形存在一种特殊关系,即一个图形绕着某点旋转一个角度可以得到另一个图形,请直接写出旋转中心的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠BAC=45°,将△ABC绕点A逆时针方向旋转得△AEF,其中,E,F是点B,C旋转后的对应点,BE,CF相交于点D.若四边形ABDF为菱形,则∠CAE的大小是( )
![]()
A. 45°B. 60°C. 75°D. 90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A(-5,0),以OA为半径作半圆,点C是第一象限内圆周上一动点,连结AC、BC,并延长BC至点D,使CD=BC,过点D作x轴垂线,分别交x轴、直线AC于点E、F,点E为垂足,连结OF.
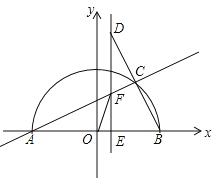
(1)当∠BAC=30时,求△ABC的面积;
(2)当DE=8时,求线段EF的长;
(3)在点C运动过程中,是否存在以点E、O、F为顶点的三角形与△ABC相似,若存在,请求出点E的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=4,以BC为直径的半圆O交斜边AB于点 D.
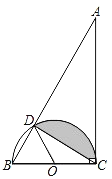
(1)证明:AD=3BD;
(2)求弧BD的长度;
(3)求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某乡镇实施产业精准扶贫,帮助贫困户承包了若干亩土地种植新品草莓,已知该草莓的成本为每千克10元,草莓成熟后投入市场销售,经市场调查发现,草莓销售不会亏本,且每天的销售量y(千克)与销售单价x(元/千克)之间函数关系如图所示.
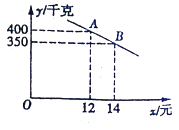
(1)求y与x的函数关系式,并写出x的取值范围.
(2)当该品种草莓的定价为多少时,每天销售获得利润最大?最大利润是多少?
(3)某村今年草莓采摘期限30天,预计产量6000千克,则按照(2)中的方式进行销售,能否销售完这批草莓?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com