
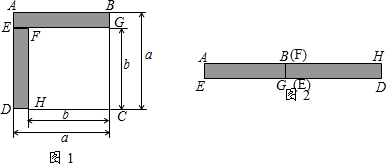
分析 (1)根据图1确定出阴影部分面积即可;
(2)根据图2确定出长方形面积即可;
(3)根据两图形面积相等得到乘法公式;
(4)利用得出的平方差公式计算即可得到结果.
解答 解:(1)根据题意得:阴影部分面积为a2-b2;
(2)根据题意得:阴影部分面积为(a+b)(a-b);
(3)可得(a+b)(a-b)=a2-b2;
(4)原式=4(1-$\frac{1}{2}$)(1+$\frac{1}{2}$)(1+$\frac{1}{{2}^{2}}$)(1+$\frac{1}{{2}^{4}}$)(1+$\frac{1}{{2}^{8}}$)+$\frac{1}{{2}^{14}}$
=4(1-$\frac{1}{{2}^{2}}$))(1+$\frac{1}{{2}^{2}}$)(1+$\frac{1}{{2}^{4}}$)(1+$\frac{1}{{2}^{8}}$)+$\frac{1}{{2}^{14}}$
=4(1-$\frac{1}{{2}^{4}}$)(1+$\frac{1}{{2}^{4}}$)(1+$\frac{1}{{2}^{8}}$)+$\frac{1}{{2}^{14}}$
=4(1-$\frac{1}{{2}^{8}}$)(1+$\frac{1}{{2}^{8}}$)+$\frac{1}{{2}^{14}}$
=4(1-$\frac{1}{{2}^{16}}$)+$\frac{1}{{2}^{14}}$
=4-$\frac{1}{{2}^{14}}$+$\frac{1}{{2}^{14}}$
=4.
故答案为:(1)a2-b2;(2)(a+b)(a-b);(3)(a+b)(a-b)=a2-b2
点评 此题考查了平方差公式的几何背景,熟练掌握平方差公式是解本题的关键.


科目:初中数学 来源: 题型:解答题
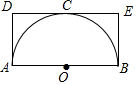 如图,AB是半圆O的直径,过半圆O上一点C的切线与过A,B两点的两条直线分别垂直相交于点D,E,若点C是劣弧$\widehat{AB}$的中点,求证:四边形ABED是矩形.
如图,AB是半圆O的直径,过半圆O上一点C的切线与过A,B两点的两条直线分别垂直相交于点D,E,若点C是劣弧$\widehat{AB}$的中点,求证:四边形ABED是矩形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
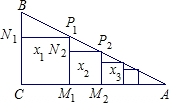 如图:Rt△ABC中,∠C=90°,BC=1,AC=2,把边长分别为x1,x2,x3,…xn的n个正方形依次放在△ABC中:第一个正方形CM1P1N1的顶点分别放在Rt△ABC的各边上;第二个正方形M1M2P2N2的顶点分别放在Rt△AP1M1的各边上,…其他正方形依次放入,则第2016个正方形的边长X2016为($\frac{2}{3}$)2016.
如图:Rt△ABC中,∠C=90°,BC=1,AC=2,把边长分别为x1,x2,x3,…xn的n个正方形依次放在△ABC中:第一个正方形CM1P1N1的顶点分别放在Rt△ABC的各边上;第二个正方形M1M2P2N2的顶点分别放在Rt△AP1M1的各边上,…其他正方形依次放入,则第2016个正方形的边长X2016为($\frac{2}{3}$)2016.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com