
 如图,在△ABC中,AD是BC边上的高,AE是BC边上的中线,cosC=$\frac{\sqrt{2}}{2}$,sinB=$\frac{1}{3}$,AD=1.
如图,在△ABC中,AD是BC边上的高,AE是BC边上的中线,cosC=$\frac{\sqrt{2}}{2}$,sinB=$\frac{1}{3}$,AD=1.分析 (1)根据cosC=$\frac{\sqrt{2}}{2}$,求出∠C=45°,根据AD=1,求出CD,根据sinB=$\frac{1}{3}$,AD=1,求出AB,根据勾股定理求出BD,得到答案;
(2)求出DE,根据正切的概念求出tan∠DAE的值.
解答 解:(1)在△ABC中,∵AD是BC边上的高,
∴∠ADB=∠ADC=90°.
∵cosC=$\frac{\sqrt{2}}{2}$,∴∠C=45°,
在△ADC中,∵∠ADC=90°,AD=1,∠C=45°,
∴DC=AD=1,
在△ADB中,∵∠ADB=90°,sinB=$\frac{AD}{AB}$=$\frac{1}{3}$,AD=1,
∴AB=3,
∴BD=$\sqrt{A{B}^{2}-A{D}^{2}}$=2$\sqrt{2}$,
∴BC=BD+DC=2$\sqrt{2}$+1.
(2)∵AE是BC边上的中线,∴CE=$\frac{1}{2}$BC=$\sqrt{2}$+$\frac{1}{2}$,
∴DE=CE-CD=$\sqrt{2}$-$\frac{1}{2}$,
∴tan∠DAE=$\frac{DE}{AD}$=$\sqrt{2}$-$\frac{1}{2}$.
点评 本题考查的是解直角三角形,掌握锐角三角函数的概念和勾股定理是解题的关键,注意要熟记特殊角的三角函数值.


 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
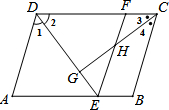 如图,在?ABCD中,∠1=∠2,∠3=∠4,EF∥AD.请直接写出与AE相等的线段FD=EF,AE=DF(两对即可),写出满足勾股定理的等式CG2+DG2=CD2(一组即可).
如图,在?ABCD中,∠1=∠2,∠3=∠4,EF∥AD.请直接写出与AE相等的线段FD=EF,AE=DF(两对即可),写出满足勾股定理的等式CG2+DG2=CD2(一组即可).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com