
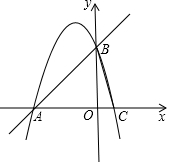
 如图,抛物线y=-x2+bx+c经过A(-3,0)、B(0,3)两点,与x轴交于另一点C.
如图,抛物线y=-x2+bx+c经过A(-3,0)、B(0,3)两点,与x轴交于另一点C.分析 (1)用待定系数法可得AB的解析式,首先设AB的解析式为:y=kx+b,再将A、B点坐标代入,解得k,b,再代入即可;
(2)将B、C点的坐标代入抛物线的解析式,解得b,c,利用抛物线与x轴的交点坐标,解得C点坐标,求得AC的长,易得△ABC的面积.
解答 解:(1)解:设直线AB的解析式为y=kx+b,
将A、B点坐标代入得,
$\left\{\begin{array}{l}{0=-3k+b}\\{3=b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=1}\\{b=3}\end{array}\right.$,
∴直线AB的解析式为:y=x+3;
(2)将B、C点的坐标代入抛物线的解析式得,
$\left\{\begin{array}{l}{0={-(-3)}^{2}-3b+c}\\{3=c}\end{array}\right.$
解得:$\left\{\begin{array}{l}{b=-2}\\{c=3}\end{array}\right.$,
∴抛物线的解析式为:y=-x2-2x+3,
令y=0,则0=-x2-2x+3,
x1=-3,x2=1,
所以C点的坐标为:(1,0),
∴|AC|=4,
∴S△ABC=$\frac{1}{2}×|AC|{×y}_{B}$=$\frac{1}{2}×4×3$=6.
点评 本题主要考查了待定系数法求解析式,解得C点的坐标是解答此题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 10g | B. | 20g | C. | 30g | D. | 40g |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
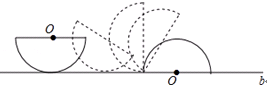 如图,半径为5的半圆的初始状态是直径平行于桌面上的直线b,然后把半圆沿直线b进行无滑动滚动,使半圆的直径与直线b重合为止,则圆心O运动路径的长度等于( )
如图,半径为5的半圆的初始状态是直径平行于桌面上的直线b,然后把半圆沿直线b进行无滑动滚动,使半圆的直径与直线b重合为止,则圆心O运动路径的长度等于( )| A. | 5π | B. | 2.5π | C. | 5+2.5π | D. | 10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com