
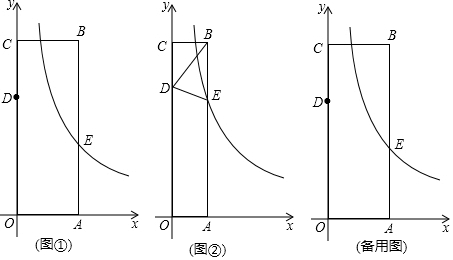
���� ��1�����ݵ�B�����������õ�E�����꣬�ɾ��ε����ʿ�֪��AB��x�ᣬ���Ե�B���E������IJ����BE�ij���
��2����ͼ�ڣ������ù��ɶ�����BD=4$\sqrt{2}$���ٷ�����������ۣ��ٵ�BD=BEʱ���ڵ�BD=DEʱ���й���m�ķ��̿ɵý��ۣ�
��3����Ϊ����OC���������⣬��������������ۣ�
�ٵ�Բ��AB����ʱ����ͼ�ۣ��������ߣ�����tan��PDQ=$\frac{1}{2}$����QH=$\frac{1}{2}$DG=2���Ӷ��ɵ�PH=1����P�ĺ�����Ϊ3������DM=OD-OM����ʽ�ɵ�m��ֵ���Ӷ��ý��ۣ�
�ڵ�Բ��OA����ʱ����ͼ�ܣ���ʱ�е�Q��A�غϣ�ͬ����AOD�ס�PGA����$\frac{PA}{AD}=\frac{PG}{OA}=\frac{AG}{OD}$=$\frac{1}{2}$����2��m-4��=$\frac{1}{4}$m+6���ɵ�m��ֵ���Ӷ��ý��ۣ�
�۵�Բ��BC����ʱ����ͼ�ݣ�
����PQ����P��PG��BC��G��ͬ���ɵã�CG=CB=4�����Դ���������������⣮
��� �⣺��1����k=16ʱ��y=$\frac{16}{x}$��
���ı���OABC�Ǿ��Σ�
��AB��OA����AB��x�ᣬ
��x=4ʱ��y=$\frac{16}{4}$=4��
��E��4��4����
�ߵ�B�������ǣ�4��$\frac{1}{4}$m+10����
��BE=$\frac{1}{4}$m+10-4=$\frac{1}{4}$m+6��
�ʴ�Ϊ��$\frac{1}{4}$m+6��
��2����ͼ�ڣ�Rt��CDB�У�CD=4��BC=4��
��BD=4$\sqrt{2}$��
�����������
�ٵ�BD=BEʱ��4$\sqrt{2}$=$\frac{1}{4}$m+6��
m=16$\sqrt{2}$-24��
�ڵ�BD=DEʱ��
��CD=4��OC=AB=$\frac{1}{4}$m+10��
��D��0��$\frac{1}{4}$m+6����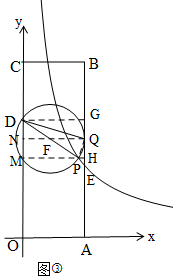
��E��4��4����
�ࣨ4$\sqrt{2}$��2=42+��$\frac{1}{4}$m+6-4��2��
m2+16m-192=0��
��m+24����m-8��=0��
m1=-24��m2=8��
��m��0��
��m=8��
��������������BDEǡ������BDΪ���ĵ��������Σ�m��ֵ��16$\sqrt{2}$-24��8��
��3�������������
�ٵ�Բ��AB����ʱ����ͼ�ۣ�
����PQ����P��MH��OA����OC��M��AB��H����MH��OC��MH��AB��
��D��DG��AB��G��ȡDP���е�F������QF�����ӳ���OC��N��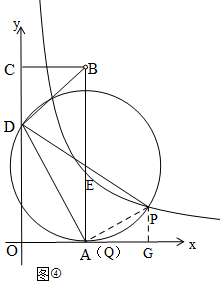
��AG=$\frac{1}{4}$m+6��
��PDΪ��F��ֱ����
���DQP=90�㣬
�á�DQG�ס�QPH��
��$\frac{DQ}{PQ}=\frac{DG}{QH}=\frac{GQ}{PH}$��
��tan��PDQ=$\frac{1}{2}$=$\frac{PQ}{DQ}$��
��$\frac{DG}{QH}=\frac{GQ}{PH}$=2��
��DG=4��
��QH=2��
������ã�P��m��$\frac{k}{m}$����
�ߡ�F��AB������Q����FQ��AB��
��NQ��MH��DG��DF=FP��
��DN=NM��QH=QG=2��
��PH=1��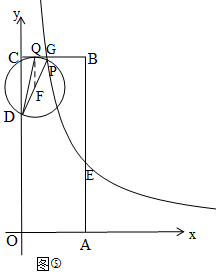
��m=MP=4-1=3��
��DM=OD-OM��
4=$\frac{1}{4}$m+6-$\frac{k}{m}$��
k=$\frac{33}{4}$��
�ڵ�Բ��OA����ʱ����ͼ�ܣ���ʱ�е�Q��A�غϣ�
����PA����P��PG��x����G��
ͬ���ɵã���AOD�ס�PGA��
��$\frac{PA}{AD}=\frac{PG}{OA}=\frac{AG}{OD}$=$\frac{1}{2}$��
��OA=4��OD=$\frac{1}{4}$m+6��AG=m-4��
��$\frac{PG}{4}=\frac{m-4}{\frac{1}{4}m+6}$=$\frac{1}{2}$��
��PG=2��2��m-4��=$\frac{1}{4}$m+6��
m=8��
��P��8��2����
��k=8��2=16��
�۵�Բ��BC����ʱ����ͼ�ݣ�
����PQ����P��PG��BC��G��
ͬ���ɵã�QG=CQ=$\frac{1}{2}$CD=2��
��CG=4��
��CB=4��
���Դ���������������⣬
�������������ڵ�P����ʱk��ֵΪ$\frac{33}{4}$��16��
���� �����Ƿ������������ۺ��⣬�����˾��ε����ʡ������ϵ����������������������Ƶ����ʺ��ж������Ǻ������������˷�������۵�˼�룬����������Բ�ܽǶ�����ֱ�����Ե�Բ�ܽ���ֱ�ǣ��������Ƶ��ж�֤����DQG�ס�QPH�ǹؼ���


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
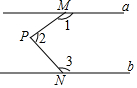 ��ͼ��a��b��M��N�ֱ���ֱ��a��b�ϣ�PΪ��ƽ�����һ�㣬��ͼ�С�1����2����3����Ĺ�ϵ�ǡ�1+��2+��3=360�㣮
��ͼ��a��b��M��N�ֱ���ֱ��a��b�ϣ�PΪ��ƽ�����һ�㣬��ͼ�С�1����2����3����Ĺ�ϵ�ǡ�1+��2+��3=360�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
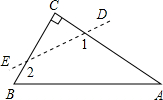 ��ͼ����ABCΪֱ�������Σ���C=90�㣬����ͼ������ȥ��C�����1+��2���ڣ�������
��ͼ����ABCΪֱ�������Σ���C=90�㣬����ͼ������ȥ��C�����1+��2���ڣ�������| A�� | 90�� | B�� | 135�� | C�� | 150�� | D�� | 270�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��Rt��ABCλ�ڵ�һ���ޣ�����ֱ�DZ�AC��AB�ֱ�ƽ����x�ᡢy�ᣬ��A������Ϊ��1��1����AB=2��AC=3��������������y=$\frac{m}{x}$��x��0����ͼ�����߶�AC�й����㣬��m��ȡֵ��ΧΪ1��m��4��
��ͼ��Rt��ABCλ�ڵ�һ���ޣ�����ֱ�DZ�AC��AB�ֱ�ƽ����x�ᡢy�ᣬ��A������Ϊ��1��1����AB=2��AC=3��������������y=$\frac{m}{x}$��x��0����ͼ�����߶�AC�й����㣬��m��ȡֵ��ΧΪ1��m��4���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
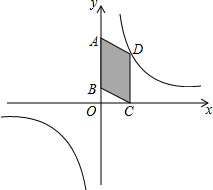 ��ͼ��ƽ���ı���ABCD��һ��AB��y���ϣ�����C��x���ϣ�����D��˫����y=$\frac{6}{x}$�ϣ���ƽ���ı���ABCD������ǣ�������
��ͼ��ƽ���ı���ABCD��һ��AB��y���ϣ�����C��x���ϣ�����D��˫����y=$\frac{6}{x}$�ϣ���ƽ���ı���ABCD������ǣ�������| A�� | 2 | B�� | 3 | C�� | 6 | D�� | 12 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com