
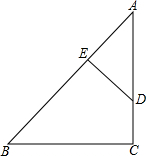
 如图,在Rt△ABC中,∠C=90°,DE⊥AB于E,$\frac{AD}{DC}$=$\frac{3}{2}$,AE•AB=15.则AC=5.
如图,在Rt△ABC中,∠C=90°,DE⊥AB于E,$\frac{AD}{DC}$=$\frac{3}{2}$,AE•AB=15.则AC=5. 分析 首先判断△ABC∽△ADE,则可得AD:AB=AE:AC,由比例式得到AD•AC=AE•AB=15,由于$\frac{AD}{DC}$=$\frac{3}{2}$,设AD=3x,CD=2x,则AC=5x,于是得到3x•5x=15,即可得到结果.
解答 解:∵∠C=90°,DE⊥AB于E,
∴∠AED=∠ACB=90°,
∵∠A=∠A,
∴△ABC∽△ADE,
∴AD:AB=AE:AC,
∴AD•AC=AE•AB=15,
∵$\frac{AD}{DC}$=$\frac{3}{2}$,
设AD=3x,CD=2x,则AC=5x,
∴3x•5x=15,
∴x=1,
∴AC=5.
故答案为:5.
点评 本题考查了相似三角形的判定与性质,熟练掌握三角形相似的判定方法并把乘积式转化成比例式是解题的关键.


科目:初中数学 来源: 题型:解答题
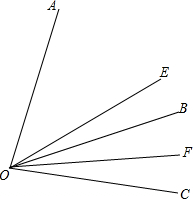 已知:如图,OC是∠AOB外的一条射线,OE平分∠AOC,OF平分∠BOC.
已知:如图,OC是∠AOB外的一条射线,OE平分∠AOC,OF平分∠BOC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
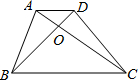 如图所示,在梯形ABCD中,AD∥BC,AD=1,BC=3,△AOD,△AOB,△BOC的面积为S1,S2,S3,那么S1:S2:S3分别等于多少?
如图所示,在梯形ABCD中,AD∥BC,AD=1,BC=3,△AOD,△AOB,△BOC的面积为S1,S2,S3,那么S1:S2:S3分别等于多少?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com