
【题目】如图,Rt△OAB的直角边OA在x轴上,顶点B的坐标为(6,8),直线CD交AB于点D(6,3),交x轴于点C(12,0).
(1)求直线CD的函数表达式;
(2)动点P在x轴上从点(﹣10,0)出发,以每秒1个单位的速度向x轴正方向运动,过点P作直线l垂直于x轴,设运动时间为t.
①点P在运动过程中,是否存在某个位置,使得∠PDA=∠B?若存在,请求出点P的坐标;若不存在,请说明理由;
②请探索当t为何值时,在直线l上存在点M,在直线CD上存在点Q,使得以OB为一边,O,B,M,Q为顶点的四边形为菱形,并求出此时t的值.

【答案】(1)直线CD的解析式为y=﹣![]() x+6;(2)①满足条件的点P坐标为(
x+6;(2)①满足条件的点P坐标为(![]() ,0)或(
,0)或(![]() ,0).②满足条件的t的值为
,0).②满足条件的t的值为![]() 或
或![]() .
.
【解析】
(1)利用待定系数法即可解决问题;
(2)①如图1中,作DP∥OB,则∠PDA=∠B.利用平行线分线段成比例定理,计算即可,再根据对称性求出P′;
②分两种情形分别求解即可解决问题:如图2中,当OP=OB=10时,作PQ∥OB交CD于Q.如图3中,当OQ=OB时,设Q(m,﹣![]() m+6),构建方程求出点Q坐标即可解决问题;
m+6),构建方程求出点Q坐标即可解决问题;
(1)设直线CD的解析式为y=kx+b,则有
![]() ,
,
解得 ,
,
∴直线CD的解析式为y=﹣![]() x+6.
x+6.
(2)①如图1中,作DP∥OB,则∠PDA=∠B.
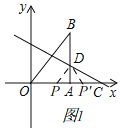
∵DP∥OB,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴OP=6﹣![]() ,
,
∴P(![]() ,0),
,0),
根据对称性可知,当AP=AP′时,P′(![]() ,0),
,0),
∴满足条件的点P坐标为(![]() ,0)或(
,0)或(![]() ,0).
,0).
②如图2中,当OP=OB=10时,作PQ∥OB交CD于Q.
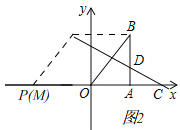
∵直线OB的解析式为y=![]() x,
x,
∴直线PQ的解析式为y=![]() x+
x+![]() ,
,
由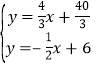 ,
,
解得![]() ,
,
∴Q(﹣4,8),
∴PQ=![]() =10,
=10,
∴PQ=OB.
∵PQ∥OB,
∴四边形OBQP是平行四边形.
∵OB=OP,
∴四边形OBQP是菱形,此时点M与的Q重合,满足条件,t=0.
如图3中,当OQ=OB时,设Q(m,﹣![]() m+6),
m+6),
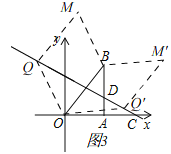
则有m2+(﹣![]() m+6)2=102,解得m=
m+6)2=102,解得m=![]() ,
,
∴点Q 的横坐标为![]() 或
或![]() ,
,
设点M的横坐标为a,则有:![]() 或
或![]() ,
,
∴a=![]() 或
或![]() ,
,
∴满足条件的t的值为![]() 或
或![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,将△ABC纸片沿DE折叠,使点A落在点A'处,且A'B平分∠ABC,A'C平分∠ACB,若∠BA'C=110°,则∠1+∠2的度数为( )

A. 80°; B. 90°; C. 100°; D. 110°;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学课上,王老师出示一道题:解方程![]() .小马立即举手并在黑板上写出了解方程过程,具体如下:
.小马立即举手并在黑板上写出了解方程过程,具体如下:
解:![]() ,
,
去括号,得:![]() .………………①
.………………①
移项,得:![]() .…………………②
.…………………②
合并同类项,得:![]() .……………………③
.……………………③
系数化为1,得:![]() .………………………④
.………………………④
(1)请你写出小马解方程过程中哪步错了,并简要说明错误原因;
(2)请你正确解方程:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴上有两个动点M,N,如果点M始终在点N的左侧,我们称作点M是点N的“追赶点”.如图,数轴上有2个点A,B,它们表示的数分别为-3,1,已知点M是点N的“追赶点”,且M,N表示的数分别为m,n.
(1)由题意得:点A是点B的“追赶点”,AB=1-(-3)=4(AB表示线段AB的长,以下相同);类似的,MN=____________.
(2)在A,M,N三点中,若其中一个点是另外两个点所构成线段的中点,请用含m的代数式来表示n.
(3)若AM=BN,MN=![]() BM,求m和n值.
BM,求m和n值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() ,
,![]() 是平面直角坐标系中的任意两点,我们把
是平面直角坐标系中的任意两点,我们把![]() 叫做P1,P2两点间的“直角距离”,记作d(P1,P2);比如:点P(2,-4),Q(1,0),则d(P,Q)=
叫做P1,P2两点间的“直角距离”,记作d(P1,P2);比如:点P(2,-4),Q(1,0),则d(P,Q)=![]() ,已知Q(2,1),动点P(x,y)满足d(P,Q)=3,且x,y均为整数,则满足条件的点P有________个.
,已知Q(2,1),动点P(x,y)满足d(P,Q)=3,且x,y均为整数,则满足条件的点P有________个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系中有 A(-2,1), B(3, 1),C(2, 3)三点,请回答下列问题:

(1)在坐标系内描出点A, B, C的位置.
(2)画出![]() 关于直线x=-1对称的
关于直线x=-1对称的![]() ,并写出
,并写出![]() 各点坐标.
各点坐标.
(3)在y轴上是否存在点P,使以A,B, P三点为顶点的三角形的面积为10?若存在,请直接写出点P的坐标:若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将直角三角形ABC沿着斜边AC的方向平移到△DEF的位置(A、D. C. F四点在同一条直线上).直角边DE交BC于点G.如果BG=4,EF=12,△BEG的面积等于4,那么梯形ABGD的面积是( )

A.16B.20C.24D.28
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上有A,B,C,D四个整数点(即各点均表示整数),且2AB=BC=3CD,若A,D两点表示的数分别为-5和6,点E为BD的中点,在数轴上的整数点中,离点E最近的点表示的数是( )
![]()
A.2B.1
C.0D.-1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com