
【题目】如图,Rt△ABC中,∠A=90°,以AB为直径的⊙O交BC于点D,点E在⊙O上, CE=CA,
AB,CE的延长线交于点F.
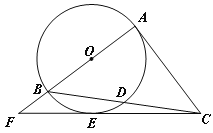
(1)求证:CE与⊙O相切;
(2)若⊙O的半径为3,EF=4,求BD的长.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)连接OE,OC,通过三角形求得证得∠OEC=∠OAC,从而证得OE⊥CF,即可证得结论;(2)根据勾股定理求得OF,解直角三角形求得tanF=OEEF=34.进而求得AC=6,从而求得△ABC是等腰直角三角形,根据勾股定理求得BC,然后根据等腰三角形三线合一的性质求得DB即可.
解:(1)连接OE,OC.
在△OEC与△OAC中,

∴△OEC≌△OAC.
∴∠OEC=∠OAC.
∵∠OAC=90°,
∴∠OEC=90°.
∴OE⊥CF于E.
∴CF与⊙O相切.
(2)解:连接AD.

∵∠OEC=90°,
∴∠OEF=90°.
∵⊙O的半径为3,
∴OE=OA=3.
在Rt△OEF中,∠OEF=90°,OE= 3,EF= 4,
∴![]() ,
,
![]() .
.
在Rt△FAC中,∠FAC=90°,![]() ,
,
∴![]() .
.
∵AB为直径,
∴AB=6=AC,∠ADB=90°.
∴BD=![]() .
.
在Rt△ABC中,∠BAC=90°,
∴![]() .
.
∴BD=![]() .
.


科目:初中数学 来源: 题型:
【题目】“重庆自然博物馆”坐落在美丽的缙云山脚下,该馆现有藏品11万余件,是全国中小学生研学实践教育基地,西大附中某数学兴趣小组,想测量博物馆的高度,他们先在博物馆正对面的大楼楼顶A处,测得博物馆底部B处的俯角为50°,测得博物馆顶端C的俯角为45°,再从楼底O经过平地到达F,再沿着斜坡向上到达E,最后经过平台达到B,测得OF=20米,平台EB的长为28.8米,已知,楼OA高为60.5米,斜坡EF的坡度i=1:2.4,A、O、F、E、B、C在同一平面内,则博物馆的高约为( )米.(参考数据:tan50°≈1.2)

A.10.5B.10.0C.12.0D.12.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中学生骑电动车上学给交通安全带来隐患,为了解某中学2 500个学生家长对“中学生骑电动车上学”的态度,从中随机调查400个家长,结果有360个家长持反对态度,则下列说法正确的是( )
A. 调查方式是普查 B. 该校只有360个家长持反对态度
C. 样本是360个家长 D. 该校约有90%的家长持反对态度
查看答案和解析>>
科目:初中数学 来源: 题型:
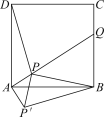
【题目】如图,点P是正方形ABCD内一点,点P到点A,B和D的距离分别为1,2![]() ,
,![]() .△ADP沿点A旋转至△ABP′,连接PP′,并延长AP与BC相交于点Q.
.△ADP沿点A旋转至△ABP′,连接PP′,并延长AP与BC相交于点Q.
(1)求证:△APP′是等腰直角三角形;
(2)求∠BPQ的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),其对称轴为直线x=1,下面结论中正确的有_____个.①abc>0,②2a﹣b=0,③4a+2b+c<0,④9a+3b+c=0
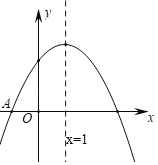
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中有三点(1,2),(3,1),(-2,-1),其中有两点同时在反比例函数![]() 的图象上,将这两点分别记为A,B,另一点记为C,
的图象上,将这两点分别记为A,B,另一点记为C,
(1)求出![]() 的值;
的值;
(2)求直线AB对应的一次函数的表达式;
(3)设点C关于直线AB的对称点为D,P是![]() 轴上的一个动点,直接写出PC+PD的最小值(不必说明理由).
轴上的一个动点,直接写出PC+PD的最小值(不必说明理由).
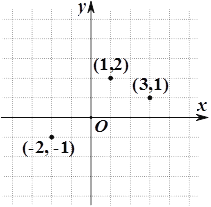
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,游客在点A处坐缆车出发,沿A﹣B﹣D的路线可至山顶D处.已知AB=BD=800米,∠α=75°,∠β=45°,求山高DE(结果精确到1米).(参考数据:sin75°=0.966,cos75°=0.259,tan75°=3.732,![]() =1.414)
=1.414)

查看答案和解析>>
科目:初中数学 来源: 题型:
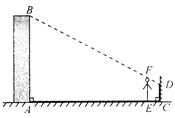
【题目】小明想利用太阳光测量楼高,他带着皮尺来到一栋楼下,发现对面墙上有这栋楼的影子,针对这种情况,他设计了一种测量方案,具体测量情况如下:如示意图,小明边移动边观察,发现站到点E处时,可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠,且高度恰好相同.此时,测得小明落在墙上的影子高度CD=1.2m,CE=0.8m,CA=30m(点A、E、C在同一直线上).已知小明的身高EF是1.7m,请你帮小明求出楼高AB(结果精确到0.1m).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com