
分析 (1)直接利用二次根式的定义得出x的取值范围;
(2)直接利用二次根式的定义得出x的取值范围;
(3)直接利用二次根式的定义得出m的取值范围;
(4)直接利用二次根式的定义得出x的取值范围.
解答 解:(1)$\sqrt{3x-4}$,
由题意可得:3x-4≥0,
解得:x≥$\frac{4}{3}$;
(2)$\frac{\sqrt{2x+1}}{1-|x|}$,
由题意可得:2x+1≥0,1-|x|≠0,
解得:x≥-$\frac{1}{2}$且x≠1;
(3)$\sqrt{{m}^{2}+4}$
由题意可得:无论m取何值,m2+4一定大于零,故m为全体实数;
(4)$\sqrt{\frac{1}{x}}$,由题意可得:x>0.
点评 此题主要考查了二次根式有意义的条件,正确把握二次根式的定义是解题关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
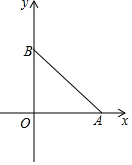 如图,在平面直角坐标系中,点O为坐标原点,A(a,0),B(0,b),且a,b满足(a-4)2+|b-4|=0,连接AB,∠OBA=45°.
如图,在平面直角坐标系中,点O为坐标原点,A(a,0),B(0,b),且a,b满足(a-4)2+|b-4|=0,连接AB,∠OBA=45°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
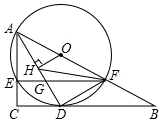 如图,在Rt△ABC中,∠C=90°,点O在AB上,经过点A的⊙O与BC相切于点D,与AC,AB分别相交于点E,F,连接AD与EF相交于点G.
如图,在Rt△ABC中,∠C=90°,点O在AB上,经过点A的⊙O与BC相切于点D,与AC,AB分别相交于点E,F,连接AD与EF相交于点G.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com