
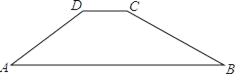
【题目】如图所示,某水库大坝的横断面是梯形ABCD,坝顶宽CD=3m,斜坡AD=8m,斜坡BC的坡度i=1:3,B,C间的水平距离为12m,则斜坡AD的坡角∠A=_____,坝底宽AB=______m.
【答案】30° (15+4![]() ).
).
【解析】
过D点作DE⊥AB于点E,过C点作CF⊥AB于点F,得到两个直角三角形和一个矩形.在Rt△BCF、Rt△AED中已知坡度和一边,或两边的比,满足解直角三角形的条件,可求出CF、DE的长度,继而根据AD=8m,可求得∠A的度数,然后解直角三角形可求得AE的长,继而也可求得AB的长度.
过D点作DE⊥AB于点E,过C点作CF⊥AB于点F,则四边形CDEF是矩形,∴CD=FE=3m,DE=CF.
∵斜坡BC的坡度i=1:3,BF=12m,∴CF:BF=1:3,则CF=![]() ×12=4m.
×12=4m.
∵AD=8m,∴sinA=DE:AD=4:8=1:2,∴∠A=30°,AE=ADcos30°=4![]() (m),∴AB=AE+EF+FB=4
(m),∴AB=AE+EF+FB=4![]() +3+12=15+4
+3+12=15+4![]() .
.
故答案为:30°,(15+4![]() ).
).


科目:初中数学 来源: 题型:
【题目】问题背景:如图1:在四边形ABCD中,AB=AD,∠BAD=120 ,∠B=∠ADC=90°.E、F分别是 BC,CD 上的点。且∠EAF=60° . 探究图中线段BE,EF,FD 之间的数量关系。 小王同学探究此问题的方法是,延长 FD 到点 G,使 DG=BE,连结 AG,先证明△ABE≌△ADG, 再证明△AEF≌△AGF,可得出结论,他的结论应是_________;
探索延伸:如图2,若四边形ABCD中,AB=AD,∠B+∠D=180° .E,F 分别是 BC,CD 上的点,且∠EAF=![]() ∠BAD,上述结论是否仍然成立,并说明理由;
∠BAD,上述结论是否仍然成立,并说明理由;
实际应用:如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东 70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以55 海里/小时的速度前进,舰艇乙沿北偏东 50°的方向以 75 海里/小时的速度前进2小时后, 指挥中心观测到甲、乙两舰艇分别到达 E,F 处,且两舰艇之间的夹角为70° ,试求此时两舰 艇之间的距离。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)叙述三角形中位线定理,并运用平行四边形的知识证明;
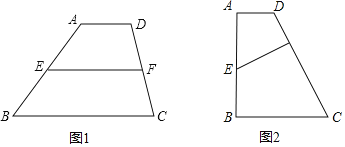
(2)运用三角形中位线的知识解决如下问题:如图1,在四边形ABCD中,AD∥BC,E、F分别是AB,CD的中点,求证:EF=![]() (AD+BC)
(AD+BC)
(3)如图2,在四边形ABCD中,AD∥BC,∠B=900,AD=3,BC=4,CD=7,E是AB的中点,直接写出点E到CD的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张明和李强两名运动爱好者周末相约进行跑步锻炼,周日早上6点,张明和李强同时从家出发,分别骑自行车和步行到离家距离分别为4.5千米和1.2千米的体育场入口汇合,结果同时到达,且张明每分钟比李强每分钟多行220米,
(1)求张明和李强的速度分别是多少米/分?
(2)两人到达体育场后约定先跑6千米再休息,李强的跑步速度是张明跑步速度的m倍,两人在同起点,同时出发,结果李强先到目的地n分钟.
①当m=1.2,n=5时,求李强跑了多少分钟?
②直接写出张明的跑步速度为多少米/分(直接用含m,n的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
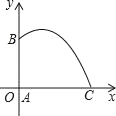
【题目】改革开放后,不少农村用上了自动喷灌设备.如图所示,AB表示水管,在B处有一个自动旋转的喷水头,一瞬间喷出的水是抛物线状,建立如图所示的直角坐标系后,抛物线的表达式为y=﹣![]() x2+2x+
x2+2x+![]() .
.
(1)当x=1时,喷出的水离地面多高?
(2)你能求出水的落地点距水管底部A的最远距离吗?
(3)水管有多高?
查看答案和解析>>
科目:初中数学 来源: 题型:
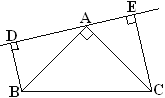
【题目】如图(1), 已知△ABC中, ∠BAC=900, AB=AC, AE是过A的一条直线, 且B、C在A、E的异侧, BD⊥AE于D, CE⊥AE于E
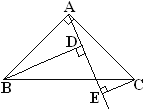
(1)试说明: BD=DE+CE.
(2)若直线AE绕A点旋转到图(2)位置时(BD<CE), 其余条件不变, 问BD与DE、CE的关系如何? 为什么?
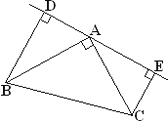
(3)若直线AE绕A点旋转到图(3)位置时(BD>CE), 其余条件不变, 问BD与DE、CE的关系如何? 请 直接写出结果, 不需说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
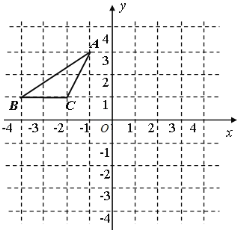
【题目】如图,在平面直角坐标系中,点A、B、C的坐标分别为(-1,3)、(-4,1)、(-2,1),先将△ABC沿一确定方向平移得到△A![]() B
B![]() C
C![]() ,点B的对应点B
,点B的对应点B![]() 的坐标是(1,2),再将△A
的坐标是(1,2),再将△A![]() B
B![]() C
C![]() 绕原点O顺时针旋转90°得到△A
绕原点O顺时针旋转90°得到△A![]() B
B![]() C
C![]() ,点A
,点A![]() 的对应点为点A
的对应点为点A![]() .
.
(1) 画出△A![]() B
B![]() C
C![]() ;
; ![]()
(2) 画出△A![]() B
B![]() C
C![]() ;
;
(3) 求出在这两次变换过程中,点A经过点A![]() 到达点A
到达点A![]() 的路径总长.
的路径总长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com