
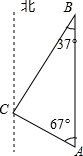
 如图,某轮船位于A处,观测到某港口城市C位于轮船的北偏西67°,轮船以21海里/时的速度向正北方向行驶,行驶5小时后该船到达B处,这时观测到城市C位于该船的南偏西37°方向,求此时轮船所处位置B与城市C的距离.
如图,某轮船位于A处,观测到某港口城市C位于轮船的北偏西67°,轮船以21海里/时的速度向正北方向行驶,行驶5小时后该船到达B处,这时观测到城市C位于该船的南偏西37°方向,求此时轮船所处位置B与城市C的距离.分析 首先过点C作CP⊥AB于点P,然后设PC=x海里,分别在Rt△APC中与Rt△PCB中,利用正切函数求得出AP与BP的长,由AB=21×5,即可得方程,解此方程即可求得x的值,继而求得答案.
解答  解:过点C作CP⊥AB于点P,
解:过点C作CP⊥AB于点P,
设PC=x海里.
在Rt△APC中,∵tan∠A=$\frac{PC}{AP}$,
∴AP=$\frac{PC}{tan67°}$=$\frac{x}{\frac{12}{5}}$=$\frac{5x}{12}$.
在Rt△PCB中,∵tan∠B=$\frac{PC}{BP}$,
∴BP=$\frac{x}{tan37°}$=$\frac{4x}{3}$,.
∵AP+BP=AB=21×5,
∴$\frac{5x}{12}$+$\frac{4}{3}$x=21×5,
解得:x=60.
∵sin∠B=$\frac{PC}{BC}$,
∴CB=$\frac{PC}{sin∠B}$=60×$\frac{5}{3}$=100(海里).
答:轮船所处位置B与城市C的距离为100海里.
点评 此题考查了方向角问题.此题难度适中,注意结合实际问题,利用解直角三角形的相关知识求解是解此题的关键,注意数形结合思想的应用.


 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源: 题型:填空题
| 栽种以后的年数n/年 | 1 | 2 | 3 | 4 | … |
| 高度h/m | 105 | 130 | 155 | 180 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 甲、乙两车从A地出发前往B地.汽车离开A地的距离 y(km)与时间t(h)的关系如图所示.
甲、乙两车从A地出发前往B地.汽车离开A地的距离 y(km)与时间t(h)的关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com