
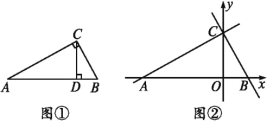
【题目】如图,在△ABC中,∠ACB=90°,CD⊥AB,
(1)图①中共有 对相似三角形,写出来分别为 (不需证明);
(2)已知AB=10,AC=8,请你求出CD的长;
(3)在(2)的情况下,如果以AB为x轴,CD为y轴,点D为坐标原点O,建立直角坐标系(如图②),若点P从点C出发,以每秒1个单位的速度沿线段CB运动,点Q从点B出发,以每秒1个单位的速度沿线段BA运动,其中一点最先到达线段的端点时,两点即刻同时停止运动;设运动时间为t秒,是否存在点P,使以点B,P,Q为顶点的三角形与△ABC相似?若存在,请求出点P的坐标;若不存在,请说明理由.
【答案】(1)3对,分别是:△ABC∽△ACD, △ABC∽△CBD , △ACD∽△CBD;(2)4.8;(3)存在,(1.35,3)或(3.15,1.8).
【解析】
试题(1)根据两角对应相等的两三角形相似即可得到3对相似三角形,分别为:△ABC∽△ACD,△ABC∽△CBD,△ABC∽△CBD;
(2)先在△ABC中由勾股定理求出BC的长,再根据△ABC的面积不变得到![]() ABCD=
ABCD=![]() ACBC,即可求出CD的长;
ACBC,即可求出CD的长;
(3)由于∠B公共,所以以点B、P、Q为顶点的三角形与△ABC相似时,分两种情况进行讨论:①△PQB∽△ACB;②△QPB∽△ACB.
试题解析:(1)图1中共有3对相似三角形,分别为:△ABC∽△ACD,△ABC∽△CBD,△ABC∽△CBD.
故答案为3,△ABC∽△ACD,△ABC∽△CBD,△ABC∽△CBD;
(2)如图1,在△ABC中,∵∠ACB=90°,AB=10,AC=8,∴BC=![]() =6.
=6.
∵△ABC的面积=![]() ABCD=
ABCD=![]() ACBC,∴CD=
ACBC,∴CD=![]() =4.8;
=4.8;
(3)存在点P,使以点B、P、Q为顶点的三角形与△ABC相似,理由如下:在△BOC中,∵∠COB=90°,BC=6,OC=4.8,∴OB=![]() =3.6.
=3.6.
分两种情况:①当∠BQP=90°时,如图2①,此时△PQB∽△ACB,
∴![]() ,∴
,∴![]() ,解得t=2.25,即BQ=CP=2.25,
,解得t=2.25,即BQ=CP=2.25,
∴OQ=OB﹣BQ=3.6﹣2.25=1.35,BP=BC﹣CP=6﹣2.25=3.75.
在△BPQ中,由勾股定理,得PQ=![]() =
=![]() ,∴点P的坐标为(1.35,3);
,∴点P的坐标为(1.35,3);

②当∠BPQ=90°时,如图2②,此时△QPB∽△ACB,∴![]() ,∴
,∴![]() ,
,
解得t=3.75,即BQ=CP=3.75,BP=BC﹣CP=6﹣3.75=2.25.
过点P作PE⊥x轴于点E.
∵△QPB∽△ACB,∴![]() ,∴
,∴![]() ,∴PE=1.8.
,∴PE=1.8.
在△BPE中,BE=![]() =
=![]() ,∴OE=OB﹣BE=3.6﹣0.45=3.15,
,∴OE=OB﹣BE=3.6﹣0.45=3.15,
∴点P的坐标为(3.15,1.8);
综上可得,点P的坐标为(1.35,3)或(3.15,1.8).



科目:初中数学 来源: 题型:
【题目】每年的6月5日为世界环保日,为了提倡低碳环保,某公司决定购买10台节省能源的新设备,现有甲、乙两种型号的设备可供选购. 经调查:购买3台甲型设备比购买2台乙型设备多花16万元,购买2台甲型设备比购买3台乙型设备少花6万元.
(1)求甲、乙两种型号设备的价格;
(2)该公司经预算决定购买节省能源的新设备的资金不超过110万元,你认为该公司有哪几种购买方案;
(3)在(2)的条件下,已知甲型设备的产量为240吨/月,乙型设备的产量为180吨/月.若每月要求总产量不低于2040吨,为了节约资金,请你为该公司设计一种最省钱的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随若移动终端设备的升级换代,手机已经成为我们生活中不可缺少的一部分,为了解中学生在假期使用手机的情况(选项:A .和同学亲友聊天;B.学习;C.购物;D.游戏;E.其它),端午节后某中学在全校范围内随机抽取了若干名学生进行调査,得到如下图表(部分信息未给出):

根据以上信息解答下列问题:
(1)这次被调查的学生有多少人?
(2)求表中![]() 的值,并补全条形统计图;
的值,并补全条形统计图;
(3)若该中学约有![]() 名学生,估计全校学生中利用手机购物或玩游戏的共有多少人?
名学生,估计全校学生中利用手机购物或玩游戏的共有多少人?
并根据以上调査结果,就中学生如何合理使用手机给出你的一条建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D在半圆O上,半径OB=2![]() ,AD=10,点C在弧BD上移动,连接AC,H是AC上一点,∠DHC=90°,连接BH,点C在移动的过程中,BH的最小值是( )
,AD=10,点C在弧BD上移动,连接AC,H是AC上一点,∠DHC=90°,连接BH,点C在移动的过程中,BH的最小值是( )

A. 5B. 6C. 7D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将两张长为5,宽为1的矩形纸条交叉,让两个矩形对角线交点重合,且使重叠部分成为一个菱形.当两张纸条垂直时,菱形周长的最小值是4,把一个矩形绕两个矩形重合的对角线交点旋转一定角度,在旋转过程中,得出所有重叠部分为菱形的四边形中,周长的最大值是( )

A. 8B. 10C. 10.4D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
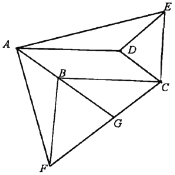
【题目】如图,在口ABCD中,分别以边BC,CD作等腰△BCF,△CDE,使BC=BF,CD=DE,∠CBF=∠CDE,连接AF,AE.
(1)求证:△ABF≌△EDA;
(2)延长AB与CF相交于G,若AF⊥AE,求证BF⊥BC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,BC=6cm,AC=8cm,点P从点C开始沿射线CA方向以1cm/s的速度运动;同时,点Q也从点C开始沿射线CB方向以3cm/s的速度运动.
(1)几秒后△PCQ的面积为3cm2?此时PQ的长是多少?(结果用最简二次根式表示)
(2)几秒后以A、B、P、Q为顶点的四边形的面积为22cm2?

查看答案和解析>>
科目:初中数学 来源: 题型:
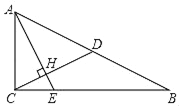
【题目】如图,在Rt△ABC中,∠ACB=9O°,CD是斜边AB上的中线,过点A作AE⊥CD,AE分别与CD、CB交于H、E两点,且AH=2CH,若AB=2![]() ,则BE的值为_____.
,则BE的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
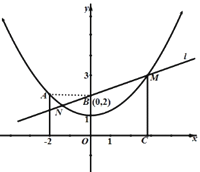
【题目】如图,已知二次函数y=ax2+1(a≠0,a为实数)的图象过点A(-2,2),一次函数y=kx+b(k≠0,k、b为实数)的图象l经过点B(0,2).
(1)求a的值并写出二次函数表达式;
(2)求b的值;
(3)设直线l与二次函数图象交于M、N两点,过M作MC垂直x轴于点C,试证明:MB=MC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com