
分析 根据非负数的性质列出关于x、y、a的方程组,然后应用加减消元法求出方程组的解即可.
解答 解:由题意得,x+y-8≥0,8-x-y≥0,
解得x+y=8,
∴$\sqrt{3x-y-a}$+$\sqrt{x-2y+a+3}$=0,
∴$\left\{\begin{array}{l}{x+y=8①}\\{3x-y-a=0②}\\{x-2y+a+3=0③}\end{array}\right.$
①+②得4x-a=8④,
①×2+③得3x+a=13⑤,
得方程组$\left\{\begin{array}{l}{4x-a=8}\\{3x+a=13}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=3}\\{a=4}\end{array}\right.$,
代入①得,y=5,
∴方程组的解为$\left\{\begin{array}{l}{x=3}\\{y=5}\\{a=4}\end{array}\right.$.
点评 本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0;还考查了三元一次方程组的解法.通过解方程组,了解把“三元”转化为“二元”、把“二元”转化为“一元”的消元的思想方法,从而进一步理解把“未知”转化为“已知”和把复杂问题转化为简单问题的思想方法.解三元一次方程组的关键是消元.解题之前先观察方程组中的方程的系数特点,认准易消的未知数,消去未知数,组成元该未知数的二元一次方程组.


科目:初中数学 来源: 题型:选择题
| A. | 不等式x<5的解有无数多个 | B. | 不等式x<5的正整数解有有限个 | ||
| C. | 不等式-3x>9的解是x<-3 | D. | 35是不等式2x<-16的一个解 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
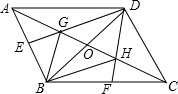 如图,已知G,H是△ABC的边AC的等分点,GE∥BH交AB于E,HF∥BG交BC于F,延长EG、FH交于D点,连接AD、DC、BD.设AC和BD交于O点,求证:四边形ABCD是平行四边形.
如图,已知G,H是△ABC的边AC的等分点,GE∥BH交AB于E,HF∥BG交BC于F,延长EG、FH交于D点,连接AD、DC、BD.设AC和BD交于O点,求证:四边形ABCD是平行四边形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com