
【题目】已知抛物线![]()
![]() 的对称轴为直线
的对称轴为直线![]() ,与x轴的一个交点坐标为(4,0),其部分图象如图所示,下列结论:
,与x轴的一个交点坐标为(4,0),其部分图象如图所示,下列结论:
①抛物线过原点;②a-b+c<0;③当x<1时,y随x增大而增大;
④抛物线的顶点坐标为(2,b);⑤若ax2+bx+c=b,则b2-4ac=0.
其中正确的是( )

A. ①②③ B. ①④⑤ C. ①②④ D. ③④⑤
【答案】B
【解析】分析: ①由抛物线的对称轴结合抛物线与x轴的一个交点坐标,可求出另一交点坐标,结论①正确;②由抛物线对称轴为2以及抛物线过原点,即可得出b=-4a、c=0,即4a+b+c=0,结论②正确;③根据抛物线的对称性结合当x=5时y>0,即可得出a-b+c>0,结论③错误;④将x=2代入二次函数解析式中结合4a+b+c=0,即可求出抛物线的顶点坐标,结论④正确;⑤观察函数图象可知,当x<2时,yy随x增大而减小,结论⑤错误.综上即可得出结论.
详解: :①∵抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=2,与x轴的一个交点坐标为(4,0),
∴抛物线与x轴的另一交点坐标为(0,0),结论①正确;
②∵抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=2,且抛物线过原点,
∴-![]() =2,c=0,
=2,c=0,
∴b=-4a,c=0,
∴4a+b+c=0,结论②正确;
③∵当x=-1和x=5时,y值相同,且均为正,
∴a-b+c>0,结论③错误;
④当x=2时,y=ax2+bx+c=4a+2b+c=(4a+b+c)+b=b,
∴抛物线的顶点坐标为(2,b),结论④正确;
⑤观察函数图象可知:当x<2时,y随x增大而减小,结论⑤错误.
综上所述,正确的结论有:①②④.
故选:C.
点睛: 本题考查了抛物线与x轴的交点、二次函数图象与系数的关系以及二次函数图象上点的坐标特征,逐一分析五条结论的正误是解题的关键.


科目:初中数学 来源: 题型:
【题目】如图,某数学兴趣小组想测量一棵树CD的高度,他们先在点A处测得树顶C的仰角为30°,然后沿AD方向前行10m,到达B点,在B处测得树顶C的仰角高度为60°(A、B、D三点在同一直线上).请你根据他们测量数据计算这棵树CD的高度(结果精确到0.1m).(参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)

【答案】8.7米
【解析】试题分析:首先利用三角形的外角的性质求得∠ACB的度数,得到BC的长度,然后在直角△BDC中,利用三角函数即可求解.
试题解析:∵∠CBD=∠A+∠ACB,
∴∠ACB=∠CBD﹣∠A=60°﹣30°=30°,
∴∠A=∠ACB,
∴BC=AB=10(米).
在直角△BCD中,CD=BCsin∠CBD=10×![]() =5
=5![]() ≈5×1.732=8.7(米).
≈5×1.732=8.7(米).
答:这棵树CD的高度为8.7米.
考点:解直角三角形的应用
【题型】解答题
【结束】
23
【题目】如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y=![]() (m≠0)的图象相交于A(2,
(m≠0)的图象相交于A(2,![]() ),B(-1,1)两点.
),B(-1,1)两点.
(1)分别求出反比例函数和一次函数的解析式;
(2)根据图象写出:当x为何值时,一次函数值大于反比例函数值?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A、B、C是数轴上三点,O为原点,点A表示的数为-12,点B表示的数为8,点C为线段AB的中点.
![]()
(1)数轴上点C表示的数是 ;
(2)点P从点A出发,以每秒2个单位长度的速度沿数轴向右匀速运动,同时,点Q从点B出发,以每秒1个单位长度的速度沿数轴向左匀速运动,当P、Q相遇时,两点都停止运动,设运动时间为t(t>0)秒.
①当t为何值时,点O恰好是PQ的中点;
②当t为何值时,点P、Q、C三个点中恰好有一个点是以另外两个点为端点的线段的三等分点(三等分点是把一条线段平均分成三等分的点).(直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农户种植一种经济作物,总用水量y(米3)与种植时间x(天)之间的函数关系式如图所示.
(1)第20天的总用水量为多少米3?
(2)当x≥20时,求y与x之间的函数关系式;
(3)种植时间为多少天时,总用水量达到7000米3?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了弘扬中华传统文化,某校组织八年级800名学生参加汉字听写大赛,为了了解学生整体听写能力,从中抽取部分学生的成绩(打分取正整数,满分100分)进行统计分析,得到如图所示的频数分布表:

请根据尚未完成的表格,解答下列问题:
(1)本次抽样调查,一共调查 名学生的成绩,表中n=
(2)补全图中所示的频数分布直方图;
(3)若成绩超过80分为优秀,则该校八年级学生中汉字听写能力优秀的约有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】感知与填空:如图①,直线![]() ,求证:
,求证:![]() .
.
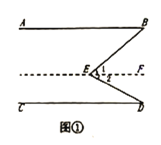
阅读下面的解答过程,并填上适当的理由,
解:过点![]() 作直线
作直线![]() ,
,
![]() ( )
( )
![]() (已知),
(已知),![]() ,
,
![]() ( )
( )
![]() ( )
( )
![]() ,
,
![]() ( )
( )
应用与拓展:如图②,直线![]() ,若
,若![]() .
.
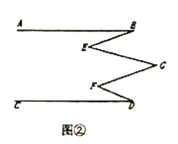
则![]() 度
度
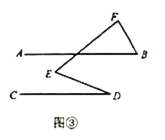
方法与实践:如图③,直线![]() ,若
,若![]() ,则
,则![]() 度.
度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:对于给定的两个函数,任取自变量x的一个值,当x<0时,它们对应的函数值互为相反数;当x0时,它们对应的函数值相等,我们称这样的两个函数互为相关函数。例如:一次函数y=x1,它们的相关函数为y=![]() .
.
(1)已知点A(5,8)在一次函数y=ax3的相关函数的图象上,求a的值;
(2)已知二次函数y=x![]() +4x
+4x![]() .
.
①当点B(m,![]() )在这个函数的相关函数的图象上时,求m的值;
)在这个函数的相关函数的图象上时,求m的值;
②当3x3时,求函数y=x![]() +4x
+4x![]() 的相关函数的最大值和最小值.
的相关函数的最大值和最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列两个等式:![]() ,
,![]() 给出定义如下:我们称使等式a﹣b=2ab﹣1成立的一对有理数a,b为“同心有理数对”,记为(a,b),如:数对(1,
给出定义如下:我们称使等式a﹣b=2ab﹣1成立的一对有理数a,b为“同心有理数对”,记为(a,b),如:数对(1,![]() ),(2,
),(2,![]() ),都是“同心有理数对”.
),都是“同心有理数对”.
(1)数对(﹣2,1),(3,![]() )是 “同心有理数对”的是__________.
)是 “同心有理数对”的是__________.
(2)若(a,3)是“同心有理数对”,求a的值;
(3)若(m,n)是“同心有理数对”,则(﹣n,﹣m) “同心有理数对”(填“是”或“不是”),说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,O为一个模拟钟面圆心,M、O、N 在一条直线上,指针 OA、OB 分别从 OM、ON 出发绕点 O 转动,OA 运动速度为每秒 30°,OB 运动速度为每秒10°,当一根指针与起始位置重合时,运动停止,设转动的时间为 t 秒,试解决下列问题:
(1)如图①,若OA顺时针转动,OB逆时针转动,![]() = 秒时,OA与OB第一次重合;
= 秒时,OA与OB第一次重合;
(2)如图②,若OA、OB同时顺时针转动,
①当![]() =3秒时,∠AOB= °;
=3秒时,∠AOB= °;
②当![]() 为何值时,三条射线OA、OB、ON其中一条射线是另两条射线夹角的角平分线?
为何值时,三条射线OA、OB、ON其中一条射线是另两条射线夹角的角平分线?



查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com