
����Ŀ��������С��ͬѧ��Ƶ����������εĸ������ij߹���ͼ�Ĺ��̣�
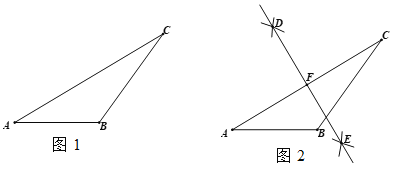
��֪����ͼ1����ABC��
������AB���ϵĸ��ߣ�
��������ͼ2��
�ٷֱ���A��CΪԲ�ģ�����![]() ��
��
Ϊ�뾶�����������ֱ��ڵ�D��E��
�� ��ֱ��DE����AC�ڵ�F��
�� �Ե�FΪԲ�ģ�FA��Ϊ�뾶��Բ����AB���ӳ����ڵ�M��
�� ����CM��
��CM Ϊ����AB���ϵĸ��ߣ�
����������ͼ���̣��ش����⣺
��1����ֱ�ߺ�Բ�棬��ȫͼ2�е�ͼ�Σ�
��2����������֤����
֤��������DA��DC��EA��EC��
������ͼ��֪DA=DC =EA=EC��
��DE���߶�AC�Ĵ�ֱƽ���ߣ�
��FA=FC ��
��AC�ǡ�F��ֱ����
���AMC=______����___________________________________���������ݣ���
��CM��AB��
��CM����AB���ϵĸ��ߣ�
���𰸡���1����ͼ����������2��90��ֱ�����Ե�Բ�ܽ���ֱ��.
��������
��1������Ҫ������ͼ�μ��ɣ�
��2�������߶εĴ�ֱƽ���ߵ������Լ�Բ�ܽǶ���֤�����ɣ�
�⣺��1����ͼ�߶�AE��Ϊ����
��2������DA��DB��EA��EB��
��DA=DB��
���D���߶�AB�Ĵ�ֱƽ�����ϣ����߶����˾�����ȵĵ��������߶εĴ�ֱƽ�����ϣ���
��EA=EB��
���E���߶�AB�Ĵ�ֱƽ�����ϣ�
��DE���߶�AB�Ĵ�ֱƽ���ߣ�
��FA=FB��
��AB�ǡ�F��ֱ����
���AGB=90����ֱ�����Ե�Բ�ܽ���ֱ������
��AG��BC
��AG����BC���ϵĸ��ߣ�
�ʴ�Ϊ��90����ֱ�����Ե�Բ�ܽ���ֱ�ǣ�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺ͬʱ����x��������A![]() ��B
��B![]() ��m��n�������������߳�Ϊͬ�������ߣ���������C1��
��m��n�������������߳�Ϊͬ�������ߣ���������C1��![]() ��������C2��
��������C2��![]() �Ƕ�����
�Ƕ�����![]() ��
��![]() ��ͬ�������ߣ�
��ͬ�������ߣ�
��1������һ����ĸ�������������C1������ͬ�������ߣ�
��2���ж�������C3��![]() ��������C1�Ƿ�Ϊͬ�������ߣ���˵�����ɣ�
��������C1�Ƿ�Ϊͬ�������ߣ���˵�����ɣ�
��3����֪������C4��C1��ͬ�������ߣ��ҹ���![]() ����������C��Ӧ���������ֵ����Сֵ��
����������C��Ӧ���������ֵ����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ΪӪ������ȫ�����������ý�ͨ��Χ,ʵʱ��ص�·����,ij�н��ܲ�����·�ڰ�װ�ĸ�������ͷ��ͼ��ʾ,����MA�����AB��ֱ,б����CD��AM���ڵ�C,���DE��AB,����ͷEF��DE�ڵ�E,AC=55��,CD=3��,EF=0.4��,��CDE=162�㡣
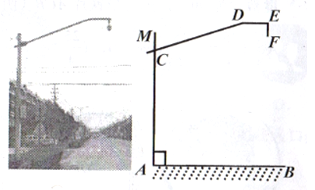
��1�����MCD�Ķ�����
��2��������ͷ�¶˵�F������AB�ľ��롣(��ȷ���ٷ�λ)
�������;sin72��=0.95��cos72���0.31,tan72��=3.08,sin18���0.31,cos18���0.95,tan18���0.32��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
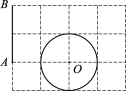
����Ŀ����ͼ��ʾ�������������������߶�AB�Ƶ�A˳ʱ����ת����0��������180���������O���У�������ֵΪ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
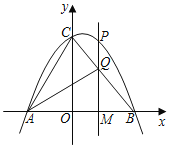
����Ŀ����ͼ��������y����![]() x2+bx+c��x����A����3��0����B��4��0�����㣬��y�ύ�ڵ�C������AC��BC��
x2+bx+c��x����A����3��0����B��4��0�����㣬��y�ύ�ڵ�C������AC��BC��
��1����������ߵı���ʽ��
��2�����B��C�����ֱ�ߵĺ�������ʽ��
��3����P�ǵ�һ�������������ϵ�һ�����㣮����P��PM��x�ᣬ����Ϊ��M��PM��BC�ڵ�Q����̽����P���˶������У��Ƿ���������ĵ�Q��ʹ����A��C��QΪ������������ǵ��������Σ������ڣ��������ʱ��P�����꣬�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ƽ��ֱ������ϵ�У���![]() �����߶�
�����߶�![]() Ϊֱ����Բ��Բ��Ϊ
Ϊֱ����Բ��Բ��Ϊ![]() ��ֱ��
��ֱ��![]() ��
��![]() �ڵ�
�ڵ�![]() ������
������![]() .
.
��1����֤��ֱ��![]() ��
��![]() �����ߣ�
�����ߣ�
��2����![]() Ϊ
Ϊ![]() ��������һ���㣬����
��������һ���㣬����![]() ��
��![]() �ڵ�
�ڵ�![]() ������
������![]() ��
��
�ٵ�![]() ʱ��������
ʱ��������![]() ������� ��ֱ��д������
������� ��ֱ��д������
����![]() �����ֵ.
�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ҵ����������ij�ֲ�Ʒ������������Ʒ�ڵ�![]() (
(![]() )����ۼ�
)����ۼ�![]() ��
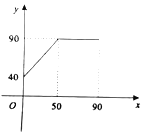
��![]() ������ϵ��ͼ��ʾ����֪����Ʒ�Ľ���Ϊÿ��30Ԫ����
������ϵ��ͼ��ʾ����֪����Ʒ�Ľ���Ϊÿ��30Ԫ����![]() ���������Ϊ
���������Ϊ![]() ����
����
��1��������ۼ�![]() ��
��![]() ֮��ĺ�����ϵ�ǣ�
֮��ĺ�����ϵ�ǣ�
��2�����������Ʒ�����۹����е��������
��3���ڸ���Ʒ���۹����У������������3600Ԫ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y��![]() x+b��b��2����x�ᣬy��ֱ���H��G���㣬�߳�Ϊ2��������OABC�ı�OA��OC�ֱ���x�ᣬy���ϣ���B�ڵ�һ���ޣ�������OABC�Ƶ�B��ʱ����ת��OA�Ķ�Ӧ��O'A'ǡ������ֱ��GH�ϣ���b��ֵΪ��������
x+b��b��2����x�ᣬy��ֱ���H��G���㣬�߳�Ϊ2��������OABC�ı�OA��OC�ֱ���x�ᣬy���ϣ���B�ڵ�һ���ޣ�������OABC�Ƶ�B��ʱ����ת��OA�Ķ�Ӧ��O'A'ǡ������ֱ��GH�ϣ���b��ֵΪ��������
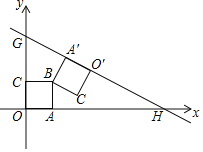
A.4![]() B.
B.![]() C.5D.6
C.5D.6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABΪ��Oֱ����CDΪ�ң�AB��CD��E������CO��AD����BAD��20�������н�������ȷ���У���������CE��OE�ڡ�C��50�� ��![]() ��
��![]() ��AD��2OE
��AD��2OE
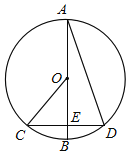
A.�٢�B.�ڢ�C.�ڢۢ�D.�٢ڢۢ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com