
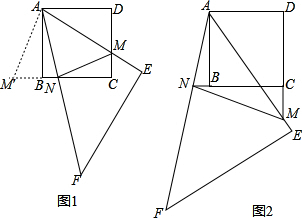
分析 (1)首先证明△ADM≌△ABM′,再证明△ANM′≌△ANM,推出MN=NM′=BN+BM′=BN+DM.
(2)以A为旋转中心,将△ADM顺时针旋转90°得到△ABM′;
(3)结论:MN=DM-BN.如图2中,以A为旋转中心,将△ADM顺时针旋转90°得到△ABM′.由△ANM′≌△ANM,可得MN=NM′,推出MN=BM′-BN=DM-BN;
解答 (1)证明:如图1中,
∵四边形ABCD是正方形,
∴AB=AD,∠D=∠ABC=90°,
∴∠ABM′=90°,
在△ADM和△ABM′中,
$\left\{\begin{array}{l}{AD=AD}\\{∠D=∠ABM′=90°}\\{DM=BM′}\end{array}\right.$,
∴△ADM≌△ABM′,
∴∠1=∠2,AM=AM′,BM′=DM,
∵∠DAB=90°,∠3=45°,
∴∠1+∠4=45°,
∴∠2+∠4=45°,
∴∠NAM′=∠3=45°,
在△AMN和△AM′N中,
$\left\{\begin{array}{l}{AN=AN}\\{∠NAM′=∠3}\\{AM′=AM}\end{array}\right.$,
∴△ANM′≌△ANM,
∴MN=NM′,
∴MN=BN+BM′=BN+DM.
(2)解:以A为旋转中心,将△ADM顺时针旋转90°得到△ABM′.
故答案为:以A为旋转中心,将△ADM顺时针旋转90°得到△ABM′.
(3)解:结论:MN=DM-BN.
理由:如图2中,以A为旋转中心,将△ADM顺时针旋转90°得到△ABM′.
同法可证:∴△ANM′≌△ANM,
∴MN=NM′,
∴MN=BM′-BN=DM-BN.
故答案为MN=DM-BN.
点评 本题考查四边形综合题、正方形的性质、全等三角形的判定和性质.旋转变换等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考压轴题.


科目:初中数学 来源: 题型:选择题
| A. | 2-3=8 | B. | -2-3=$\frac{1}{8}$ | C. | -2-3=-$\frac{1}{8}$ | D. | (2017-π)0=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
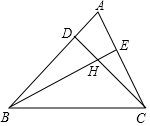 如图锐角△ABC,若∠ABC=40°,∠ACB=70°,点D、E在边AB、AC上,CD与BE交于点H.
如图锐角△ABC,若∠ABC=40°,∠ACB=70°,点D、E在边AB、AC上,CD与BE交于点H.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
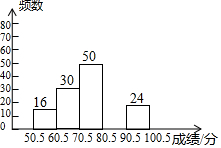 某校组织1000名学生参加“青少年普法知识大赛”,为了了解学生的参赛成绩,从中抽取部分学生的参赛成绩(成绩均为整数)进行统计,并绘制成如下的不完全统计图表.
某校组织1000名学生参加“青少年普法知识大赛”,为了了解学生的参赛成绩,从中抽取部分学生的参赛成绩(成绩均为整数)进行统计,并绘制成如下的不完全统计图表.| 组别 | 分数段 | 频数 | 频率 |
| 一 | 50.5-60.5 | 16 | 0.08 |
| 二 | 60.5-70.5 | 30 | 0.15 |
| 三 | 70.5-80.5 | 50 | 0.25 |
| 四 | 80.5-90.5 | m | 0.40 |
| 五 | 90.5-100.5 | 24 | n |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,A、B分别是x轴上位于原点左右两侧的两点,点P(a,4)在第一象限内,一过原点的直线y=2x与直线BD、直线AC同时过点P,直线BD交y轴于点D,且线段AO=2.
如图,A、B分别是x轴上位于原点左右两侧的两点,点P(a,4)在第一象限内,一过原点的直线y=2x与直线BD、直线AC同时过点P,直线BD交y轴于点D,且线段AO=2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
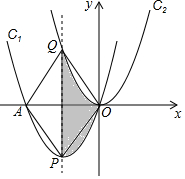 如图,在平面直角坐标系xOy中,抛物线C1的顶点为P(-3,-$\frac{9}{2}$),且过点O(0,0).
如图,在平面直角坐标系xOy中,抛物线C1的顶点为P(-3,-$\frac{9}{2}$),且过点O(0,0).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com