
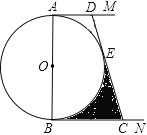
【题目】如图,AB是⊙O的直径,AM和BN是⊙O的两条切线,E为⊙O上一点,过点E作直线DC分别交AM,BN于点D,C,且CB=CE.
(1)求证:DA=DE;
(2)若AB=6,CD=4![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
【答案】(1)证明见解析;(2)![]()
【解析】(1)连接OE,BE,根据已知条件证明CD为⊙O的切线,然后再根据切线长定理即可证明DA=DE;
(2) 如图,连接OC,过点D作DF⊥BC于点F,根据S阴影部分=S四边形BCEO﹣S扇形OBE,利用分割法即可求得阴影部分的面积.
(1)如图,连接OE、BE,
∵OB=OE,
∴∠OBE=∠OEB.
∵BC=EC,
∴∠CBE=∠CEB,
∴∠OBC=∠OEC.
∵BC为⊙O的切线,
∴∠OEC=∠OBC=90°;
∵OE为半径,
∴CD为⊙O的切线,
∵AD切⊙O于点A,
∴DA=DE;
(2)如图,连接OC,过点D作DF⊥BC于点F,则四边形ABFD是矩形,
∴AD=BF,DF=AB=6,
∴DC=BC+AD=4![]() ,
,
∵CF=![]() =2
=2![]() ,
,
∴BC﹣AD=2![]() ,
,
∴BC=3![]() ,
,
在直角△OBC中,tan∠BOC=![]() =
=![]() ,
,
∴∠BOC=60°.
在△OEC与△OBC中,
 ,
,
∴△OEC≌△OBC(SSS),
∴∠BOE=2∠BOC=120°,
∴S阴影部分=S四边形BCEO﹣S扇形OBE=2×![]() BCOB﹣
BCOB﹣![]() =9
=9![]() ﹣3π.
﹣3π.



科目:初中数学 来源: 题型:
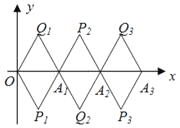
【题目】如图,菱形OP1A1Q1为长为2,且∠P1=60°,将菱形OP1A1Q1绕点A1顺时针旋转1800,得到菱形A1P2A2Q2,将菱形A1P2A2Q2绕点A2顺时针旋转180°,得到菱形A2P3A3Q3……,如此进行下去,直至得到菱形A8P9A9Q9,则:
(1)P1的坐标为_____;
(2)Q9的坐标为_____;
查看答案和解析>>
科目:初中数学 来源: 题型:
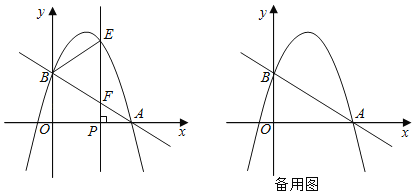
【题目】如图,在平面直角坐标系中,直线![]() 分别交x轴,y轴于点A,B,抛物线y=﹣x2+bx+c经过点A,B,点P是x轴上一个动点,过点P作垂直于x轴的直线分别交抛物线和直线AB于点E和点F.设点P的横坐标为m.
分别交x轴,y轴于点A,B,抛物线y=﹣x2+bx+c经过点A,B,点P是x轴上一个动点,过点P作垂直于x轴的直线分别交抛物线和直线AB于点E和点F.设点P的横坐标为m.
(1)求这条抛物线所对应的函数表达式.
(2)点P在线段OA上时,若以B、E、F为顶点的三角形与△FPA相似,求m的值;
(3)若E、F、P三个点中恰有一点是其它两点所连线段的中点(三点重合除外),称E、F、P三点为“共诸点”.直接写出E、F、P三点成为“共诸点”时m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在直角坐标系中,点A的坐标为(1,0),以OA为边在第一象限内作正方形OABC,点D是x轴正半轴上一动点(OD>1),连接BD,以BD为边在第一象限内作正方形DBFE,设M为正方形DBFE的中心,直线MA交y轴于点N.如果定义:只有一组对角是直角的四边形叫做损矩形.
(1)试找出图1中的一个损矩形;
(2)试说明(1)中找出的损矩形的四个顶点一定在同一个圆上;
(3)随着点D位置的变化,点N的位置是否会发生变化?若没有发生变化,求出点N的坐标;若发生变化,请说明理由;
(4)在图②中,过点M作MG⊥y轴于点G,连接DN,若四边形DMGN为损矩形,求D点坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
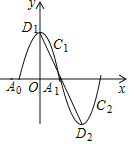
【题目】如图,一段抛物线y=﹣x2+4(﹣2≤x≤2)为C1,与x轴交于A0,A1两点,顶点为D1;将C1绕点A1旋转180°得到C2,顶点为D2;C1与C2组成一个新的图象,垂直于y轴的直线l与新图象交于点P1(x1,y1),P2(x2,y2),与线段D1D2交于点P3(x3,y3),设x1,x2,x3均为正数,t=x1+x2+x3,则t的取值范围是( )
A. 6<t≤8 B. 6≤t≤8 C. 10<t≤12 D. 10≤t≤12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中2条直线,分别为![]()
![]() ,
,![]()
![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 轴的平行线交
轴的平行线交![]() 于点
于点![]() ,抛物线
,抛物线![]() 过
过![]() 、
、![]() 、
、![]() 三点.
三点.
下列判断中:
①![]() ;
;
②抛物线关于直线![]() 轴对称 ;
轴对称 ;
③点![]() 在抛物线上方;
在抛物线上方;
④![]() ;
;
⑤![]() .其中正确的个数有( )
.其中正确的个数有( )
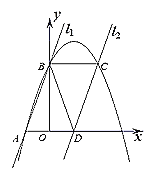
A.5B.4C.3D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
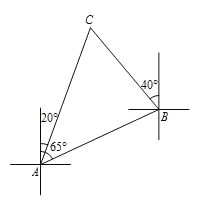
【题目】如图,一艘船由A港沿北偏东65°方向航行![]() km至B港,然后再沿北偏西40°方向航行至C港,C港在A港北偏东20°方向.
km至B港,然后再沿北偏西40°方向航行至C港,C港在A港北偏东20°方向.
求:(1)∠C的度数;
(2)A,C两港之间的距离为多少km.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年5月,以“寻根国学,传承文明”为主题的兰州市第三届“国学少年强一国学知识挑战赛”总决赛拉开帷幕,小明晋级了总决赛.比赛过程分两个环节,参赛选手须在每个环节中各选择一道题目.
第一环节:写字注音、成语故事、国学常识、成语接龙(分别用![]() 表示);
表示);
第二环节:成语听写、诗词对句、经典通读(分别用![]() 表示)
表示)
(1)请用树状图或列表的方法表示小明参加总决赛抽取题目的所有可能结果
(2)求小明参加总决赛抽取题目都是成语题目(成语故事、成语接龙、成语听写)的概率。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com