
 如图,在△ABC中,∠C=90°,∠A=30°,BC=5,在△DEF中,∠EDF=90°,∠DEF=45°,DE=3.现将△DEF的直角边DF与△ABC的斜边AB重合在一起,并将△DEF沿AB方向移动,在移动过程中,D、F两点始终在AB边上(移动开始时点D与点A重合,一直移动到点F与点B重合为止),连接BE,设AD=x,BE=y.下列结论:①当x=2时,y=$\sqrt{73}$;②当x=10-4$\sqrt{3}$时,BE∥AC;③当x=7-3$\sqrt{2}$时,∠EBD=22.5°,其中正确有( )
如图,在△ABC中,∠C=90°,∠A=30°,BC=5,在△DEF中,∠EDF=90°,∠DEF=45°,DE=3.现将△DEF的直角边DF与△ABC的斜边AB重合在一起,并将△DEF沿AB方向移动,在移动过程中,D、F两点始终在AB边上(移动开始时点D与点A重合,一直移动到点F与点B重合为止),连接BE,设AD=x,BE=y.下列结论:①当x=2时,y=$\sqrt{73}$;②当x=10-4$\sqrt{3}$时,BE∥AC;③当x=7-3$\sqrt{2}$时,∠EBD=22.5°,其中正确有( )| A. | 3个 | B. | 2个 | C. | 1个 | D. | 0个 |
分析 由在△ABC中,∠C=90°,∠A=30°,BC=5,可求得AB的长,然后由当x=2时,求得BD的长,利用勾股定理即可求得BE的长;由当x=10-4$\sqrt{3}$时,可求得BD的长,利用三角函数的知识即可求得∠EBD<30°,即可知BE与AC不平行;由当x=7-3$\sqrt{2}$时,易求得EF=BF,继而求得∠EBD=22.5°.
解答 解:∵在△ABC中,∠C=90°,∠A=30°,BC=5,
∴AB=2BC=10,
①∵AD=x=2,
∴BD=AB-AD=8,
∴y=BE=$\sqrt{D{E}^{2}+D{B}^{2}}$=$\sqrt{73}$;故正确;
②当x=10-4$\sqrt{3}$时,BD=4$\sqrt{3}$,
∴tan∠EBD=$\frac{DE}{BD}$=$\frac{\sqrt{3}}{4}$,
∴∠EBD<30°≠∠A,
∴BE与AC不平行;故错误;
③当x=7-3$\sqrt{2}$时,BD=3$\sqrt{2}$+3,
∴BF=BD-DF=3$\sqrt{2}$,
∵EF=$\sqrt{2}$DE=3$\sqrt{2}$,
∴EF=BF,
∴∠EBD=$\frac{1}{2}$∠EFD=22.5°;正确.
故选B.
点评 此题属于三角形的综合题.考查了勾股定理、三角函数、等腰三角形的判定与性质以及平行线的判定等知识.注意根据题意求得BD的长是关键.


科目:初中数学 来源: 题型:解答题
 已知:如图,AB∥DC,AC和BD相交于点O,E是CD上一点,F是OD上一点,且∠1=∠A.
已知:如图,AB∥DC,AC和BD相交于点O,E是CD上一点,F是OD上一点,且∠1=∠A.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 《孙子算经》是中国传统数学最重要的著作,约成书于四、五世纪.现在传本的《孙子算经》共三卷.卷上叙述算筹记数的纵横相间制度和筹算乘除法则;卷中举例说明筹算分数算法和筹算开平方法;卷下记录算题,不但提供了答案,而且还给出了解法.其中记载:“今有木,不知长短.引绳度之,余绳四尺五,屈绳量之,不足一尺.问木长几何?”
《孙子算经》是中国传统数学最重要的著作,约成书于四、五世纪.现在传本的《孙子算经》共三卷.卷上叙述算筹记数的纵横相间制度和筹算乘除法则;卷中举例说明筹算分数算法和筹算开平方法;卷下记录算题,不但提供了答案,而且还给出了解法.其中记载:“今有木,不知长短.引绳度之,余绳四尺五,屈绳量之,不足一尺.问木长几何?”查看答案和解析>>
科目:初中数学 来源: 题型:填空题
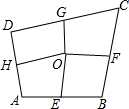 如图,四边形ABCD中,E、F、G、H依次是各边中点,O是形内一点,若S四边形AEOH=4,S四边形BFOE=5,S四边形CGOF=6,则S四边形DHOG=5.
如图,四边形ABCD中,E、F、G、H依次是各边中点,O是形内一点,若S四边形AEOH=4,S四边形BFOE=5,S四边形CGOF=6,则S四边形DHOG=5.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com