
【题目】为了了解我市中学生跳绳活动开展的情况,随机抽查了全市八年级部分同学1分钟跳绳的次数,将抽查结果进行统计,并绘制成如下的两个不完整的统计图:

请根据图中提供的信息,解答下列问题:
(1)本次共抽查了多少名学生?请补全频数分布直方图;
(2)若本次抽查中,跳绳次数在125次以上(含125次)为优秀,请你估计全市8000名八年级学生中有多少名学生的成绩为优秀;
(3)请你根据以上信息,对我市开展的学生跳绳活动情况谈谈自己的看法或建议.
【答案】(1)200 名,补全图见解析;(2)4200名;(3)见解析.
【解析】
(1)利用95≤x<115的人数是8+16=24人,所占的比例是12%即可求解;总人数减去其余范围的人数求得135≤x<145的人数,据此补全图形可得;
(2)首先求得所占的比例,然后乘以总人数8000即可求解.
(3)全市达到优秀的人数有一半以上,反映了我市学生锻炼情况很好.
(1)本次调查的总人数为(8+16)÷12%=200(人);
135≤x<145的人数为200-(8+16+71+60+16)=29,
补全条形图如下:

(2)![]() .
.
答:估计全市8000名八年级学生中有4200名学生的成绩为优秀.
(3)全市达到优秀的人数有一半以上,反映了我市学生锻炼情况很好.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】今年春北方严重干旱,某社区人畜饮水紧张,每天需从社区外调运饮用水120吨,有关部门紧急部署,从甲、乙两水厂调运饮用水到社区供水点,甲厂每天最多可调出80吨,乙厂每天最多可调出90吨,从两水厂运水到社区供水点的路程和运费如下表:
到社区供水点的路程(千米) | 运费(元/吨·千米) | |
甲厂 | 20 | 12 |
乙厂 | 14 | 15 |
【1】若某天调运水的总运费为26700元,则从甲、乙两水厂各调运多少吨饮用水?
【2】设从甲厂调运饮用水![]() 吨,总运费为W元,试写出W关于与
吨,总运费为W元,试写出W关于与![]() 的函数关系式,怎样安排调运方案才能使每天的总运费最省?
的函数关系式,怎样安排调运方案才能使每天的总运费最省?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某市2019年11月21日---11月27日最高气温走势图,则下列说法不正确的是( )

A.21日---22日的最高气温呈上升趋势
B.这7天中,23日的最高气温高于其他6天的的最高气温
C.23---25日的最高气温呈下降趋势
D.相邻两天中,24日---25日的最高气温变化最大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在宽20米,长32米的矩形耕地上,修筑同样宽的三条路(两条纵向,一条横向,并且横向与纵向互相垂直),把这块耕地分成大小相等的六块试验田,要使试验田的面积是570平方米,问道路应该多宽?

查看答案和解析>>
科目:初中数学 来源: 题型:
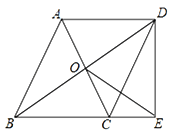
【题目】如图,□ABCD的对角线交于点O,点E在边BC的延长线上,且OE=OB,连接DE.
(1)求证:△BDE是直角三角形;
(2)如果OE⊥CD,试判断△BDE与△DCE是否相似,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于点
的图象交于点![]() 和
和![]() ,与y轴交于点C.
,与y轴交于点C.
(1)![]() = ,
= ,![]() = ;
= ;
(2)根据函数图象可知,当![]() >
>![]() 时,x的取值范围是 ;
时,x的取值范围是 ;
(3)过点A作AD⊥x轴于点D,点P是反比例函数在第一象限的图象上一点.设直线OP与线段AD交于点E,当![]() :
:![]() =3:1时,求点P的坐标.
=3:1时,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=kx2+2kx﹣3k(k≠0),的图象与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,且OC=OA.
(1)点A坐标为 ,点B坐标为 ,抛物线的解析式为 ;
(2)若点P是第二象限内抛物线上的一个动点,连接AP、CP,当四边形ABCP的面积最大时,求点P的坐标;
(3)若点Q(0,m)是y轴上的动点,连接AQ、BQ,
①当∠AQB是钝角时,求m的取值范围;
②当∠AQB=60°时,则m= .(直接写出答案)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲船从A处起以15海里/小时的速度向正北方向航行,这时乙船从A的正东方向20海里的B处以20海里/小时的速度向正西方向航行.
(1)多长时间后,两船相距15海里?
(2)多长时间后,两船的距离最小?最小距离是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①,直线AB//CD,试确定∠B,∠BPC,∠C之间的数量关系:
(2)如图②,直线AB//CD.∠ABP与∠DCP的平分线相交于点P1,请确定∠P与∠P1的数量关系;
(3)如图③,若∠A=![]() (0<
(0<![]() <180°,且
<180°,且![]() ≠135°),点B点C分别在∠A的两边上,分别过点B和点C作直线
≠135°),点B点C分别在∠A的两边上,分别过点B和点C作直线![]() 和
和![]() .使得,
.使得,![]() 、
、![]() 分别与AB,AC的夹角为
分别与AB,AC的夹角为![]() .且
.且![]() 和
和![]() 交于点O,请直接写出∠BOC的度数.
交于点O,请直接写出∠BOC的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com