
分析 (1)根据“吉样数”的定义,由既能被2整除又能被3整除的数的特征求解即可;
(2)根据“吉样数”的定义,可得d是偶数,根据偶数的定义可知4(a+b+c)是偶数,从而求解;
(3)d+4(a+b+c)=a+b+c+d+3(a+b+c),通过证明“吉样数”的定义得出a+b+c+d能被3整除,结合(2)即可求解.
解答 解:(1)∵7+8+5=20,$\overline{785x}$是“吉样数”,
∴$\overline{785x}$中x只能为4;
(2)∵正整数$\overline{abcd}$是“吉样数”,
∴d是偶数,
∵4(a+b+c)是偶数,
∴d+4(a+b+c)是偶数,
∴d+4(a+b+c)能被2整除;
(3)对,
由(2)知d+4(a+b+c)能被2整除,
∵四位正整数$\overline{abcd}$是“吉样数”,
∴a+b+c+d能被3整除,
即a+b+c+d=3x,x为正整数,
∴d+4(a+b+c)
=a+b+c+d+3(a+b+c)
=3x+3(a+b+c)
=3(a+b+c+x),
∴d+4(a+b+c)能被3整除.
综上所述,d+4(a+b+c)是“吉祥数字”.
点评 考查了因式分解的应用,解题的关键是理解阅读材料的内容,以及理解“吉样数”的定义.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
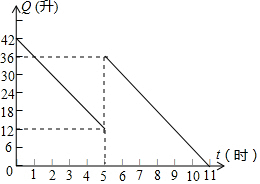 某机动车出发前油箱内有油42升,行驶若干小时后,途中在加油站加油若干升,油箱中余油量Q(升)与行驶时间t(时)之间的函数关系如图所示,回答下列问题.
某机动车出发前油箱内有油42升,行驶若干小时后,途中在加油站加油若干升,油箱中余油量Q(升)与行驶时间t(时)之间的函数关系如图所示,回答下列问题.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m≤0 | B. | 0≤m≤$\frac{1}{2}$ | C. | m≤$\frac{1}{2}$ | D. | m>$\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
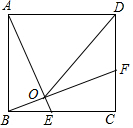 如图,在正方形ABCD中,AB=5.点E为BC边上一点(不与点B重合),点F为CD边上一点,线段AE、BF相交于点O,其中AE=BF.
如图,在正方形ABCD中,AB=5.点E为BC边上一点(不与点B重合),点F为CD边上一点,线段AE、BF相交于点O,其中AE=BF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com