
【题目】如图,在![]() 中,
中, ![]() .在同一平面内,
.在同一平面内,![]() 内部一点
内部一点![]() 到
到![]() 的距离都等于
的距离都等于![]() (
(![]() 为常数),到点
为常数),到点![]() 的距离等于
的距离等于![]() 的所有点组成图形
的所有点组成图形![]() .
.
(1)直接写出![]() 的值;
的值;
(2)连接![]() 并延长,交
并延长,交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() .
.
①求证:![]() ;
;
②求直线![]() 与图形
与图形![]() 的公共点个数.
的公共点个数.
【答案】(1)![]() ;(2)①见解析;②直线
;(2)①见解析;②直线![]() 与图形
与图形![]() 的公共点个数为1
的公共点个数为1
【解析】
(1)连接OA,OB,OC,推出∠A=90°,再根据S△ABC=S△AOB+S△BOC+S△AOC列式求解即可;
(2)根据题意得出OB平分∠ABC,即![]() ,再根据
,再根据![]() ,即可证明
,即可证明![]() ;
;
(3)设![]() 与
与![]() 的切点为
的切点为![]() ,连接
,连接![]() ,作
,作![]() 于点
于点![]() ,证明
,证明![]() 即可得出答案.
即可得出答案.
解:(1)连接OA,OB,OC,
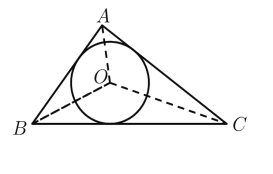
∵AB=3,AC=4,BC=5,
∴AB2+AC2=BC2,
∴∠BAC=90°,
∴S△ABC=![]() ABAC=
ABAC=![]() ×3×4=6,
×3×4=6,
∵S△ABC=S△AOB+S△BOC+S△AOC
=![]() (AB+AC+BC)×a
(AB+AC+BC)×a
=![]() (3+4+5)×a
(3+4+5)×a
∴![]() ×12a=6
×12a=6
∴a=1;
(2)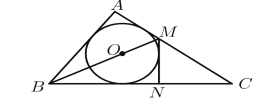
①由题意可知图形![]() 是以
是以![]() 为圆心,
为圆心,![]() 为半径的圆,
为半径的圆,![]() 与
与![]() 相切,
相切,
∵点O到AB、BC的距离为1,
∴OB平分∠ABC,
∴![]() ,
,
∵![]() ,
,
∴∠A=90°,
∵![]() ,
,
∴![]() ,
,
∴∠BMA=90°-∠ABM,
∠BMN=90°-∠NBM,
∴![]() ;
;
②如图,设![]() 与
与![]() 的切点为
的切点为![]() ,连接
,连接![]() ,作
,作![]() 于点
于点![]() ,
,
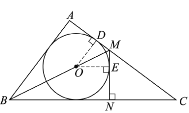
∵![]() ,OE⊥MN,
,OE⊥MN,
∴∠ODM=∠OEM,
由①可知∠BMA=∠BMN,
又∵OM=OM,
∴△ODM≌△OEM,
∴![]() ,
,
∴![]() 为
为![]() 的半径,
的半径,
∴![]() 为
为![]() 的切线,
的切线,
∴直线![]() 与图形
与图形![]() 的公共点个数为1.
的公共点个数为1.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源: 题型:
【题目】五张完全相同的卡片的正面分别画有等边三角形、平行四边形、矩形、菱形、正方形,将其背面朝上放在桌面上,从中随机抽取一张,所抽取的卡片上的图形既是轴对称图形,又是中心对称图形的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
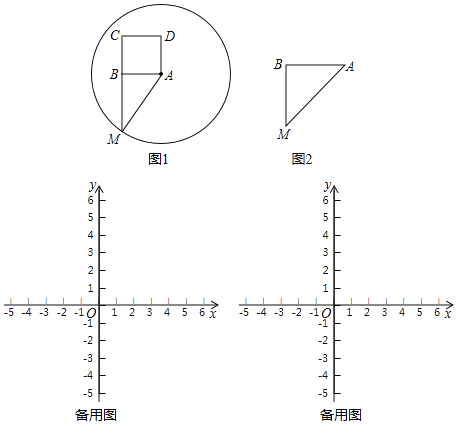
【题目】在△ABM中,∠ABM=90°,以AB为一边向△ABM的异侧作正方形ABCD,以A为圆心,AM为半径作⊙A,我们称正方形ABCD为⊙A的“关于△ABM的友好正方形”,如果正方形ABCD恰好落在⊙A的内部(或圆上),我们称正方形ABCD为⊙A的“关于△ABM的绝对友好正方形”,例如,图1中正方形ABCD是⊙A的“关于△ABM的友好正方形”.
(1)图2中,△ABM中,BA=BM,∠ABM=90°,在图中画出⊙A的“关于△ABM的友好正方形ABCD”.
(2)若点A在反比例函数y=![]() (k>0,x>0)上,它的横坐标是2,过点A作AB⊥y轴于B,若正方形ABCD为⊙A的“关于△ABO的绝对友好正方形”,求k的取值范围.
(k>0,x>0)上,它的横坐标是2,过点A作AB⊥y轴于B,若正方形ABCD为⊙A的“关于△ABO的绝对友好正方形”,求k的取值范围.
(3)若点A是直线y=﹣x+2上的一个动点,过点A作AB⊥y轴于B,若正方形ABCD为⊙A的“关于△ABO的绝对友好正方形”,求出点A的横坐标m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AC,BD交于点O,且AO=BO.
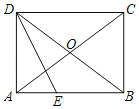
(1)求证:四边形ABCD是矩形;
(2)∠ADB的角平分线DE交AB于点E,当AD=3,tan∠CAB=![]() 时,求AE的长.
时,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=kx2+(2k+1)x+1(k为实数).
(1)对于任意实数k,函数图象一定经过点(﹣2,﹣1)和点_____;
(2)对于任意正实数k,当x>m时,y随着x的增大而增大,写出一个满足题意的m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,点
中,点![]() ,若射线
,若射线![]() 上存在点
上存在点![]() ,使得
,使得![]() 是以
是以![]() 为腰的等腰三角形,就称点
为腰的等腰三角形,就称点![]() 为线段
为线段![]() 关于射线
关于射线![]() 的等腰点.
的等腰点.
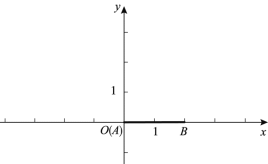
(1)如图, ![]() ,
,
①若![]() ,则线段
,则线段![]() 关于射线
关于射线![]() 的等腰点的坐标是_____;
的等腰点的坐标是_____;
②若![]() ,且线段
,且线段![]() 关于射线
关于射线![]() 的等腰点的纵坐标小于1,求
的等腰点的纵坐标小于1,求![]() 的取值范围;
的取值范围;
(2) 若![]() ,且射线
,且射线![]() 上只存在一个线段
上只存在一个线段![]() 关于射线
关于射线![]() 的等腰点,则
的等腰点,则![]() 的取值范围是__________.
的取值范围是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
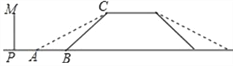
【题目】某地的一座人行天桥如图所示,天桥高为6米,坡面BC的坡度为1:1,为了方便行人推车过天桥,有关部门决定降低坡度,使新坡面的坡度为1:![]() .
.
(1)求新坡面的坡角∠CAB的度数;
(2)原天桥底部正前方8米处(PB的长)的文化墙PM是否需要拆除?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人进行摸牌游戏,现有三张形状大小完全相同的牌,正面分别标有数字![]() ,
,![]() ,
,![]() ,将三张牌背面朝上,洗匀后放在桌子上.
,将三张牌背面朝上,洗匀后放在桌子上.
(1)甲从中随机抽取一张牌,记录数字后放回洗匀,乙再随机抽取一张.请用列表法或画树状图的方法写出所有可能的结果;
(2)若两人抽取的数字和为![]() 的倍数,则甲获胜;若抽取的数字和为
的倍数,则甲获胜;若抽取的数字和为![]() 的倍数,则乙获胜,这个游戏公平吗?请用概率的知识加以解释.
的倍数,则乙获胜,这个游戏公平吗?请用概率的知识加以解释.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com