
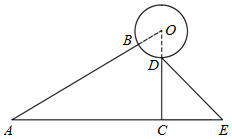
 某太阳能热水器的横截面示意图如图所示,已知真空热水管AB与支架CD所在直线相交于点O,且OB=OD,支架CD与水平线AE垂直,∠BAC=∠CDE=30°,DE=80cm,AC=165cm.
某太阳能热水器的横截面示意图如图所示,已知真空热水管AB与支架CD所在直线相交于点O,且OB=OD,支架CD与水平线AE垂直,∠BAC=∠CDE=30°,DE=80cm,AC=165cm.分析 (1)在Rt△CDE中,根据∠CDE=30°,DE=80cm,求出支架CD的长是多少即可.
(2)首先在Rt△OAC中,根据∠BAC=30°,AC=165cm,求出OC的长是多少,进而求出OD的长是多少;然后求出OA的长是多少,即可求出真空热水管AB的长是多少.
解答 解:(1)在Rt△CDE中,∠CDE=30°,DE=80cm,
∴CD=80×cos30°=80×$\frac{\sqrt{3}}{2}$=40$\sqrt{3}$(cm).
(2)在Rt△OAC中,∠BAC=30°,AC=165cm,
∴OC=AC×tan30°=165×$\frac{\sqrt{3}}{3}$=55$\sqrt{3}$(cm),
∴OD=OC-CD=55$\sqrt{3}$-40$\sqrt{3}$=15$\sqrt{3}$(cm),
∴AB=AO-OB=AO-OD=55$\sqrt{3}$×2-15$\sqrt{3}$=95$\sqrt{3}$(cm).
点评 此题主要考查了解直角三角形的应用,要熟练掌握,注意将实际问题抽象为数学问题(画出平面图形,构造出直角三角形转化为解直角三角形问题).


科目:初中数学 来源: 题型:填空题
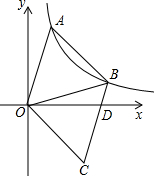 如图,已知等边三角形OAB与反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象交于A、B两点,将△OAB沿直线OB翻折,得到△OCB,点A的对应点为点C,线段CB交x轴于点D,则$\frac{BD}{DC}$的值为$\frac{\sqrt{3}-1}{2}$.(已知sin15°=$\frac{\sqrt{6}-\sqrt{2}}{4}$)
如图,已知等边三角形OAB与反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象交于A、B两点,将△OAB沿直线OB翻折,得到△OCB,点A的对应点为点C,线段CB交x轴于点D,则$\frac{BD}{DC}$的值为$\frac{\sqrt{3}-1}{2}$.(已知sin15°=$\frac{\sqrt{6}-\sqrt{2}}{4}$)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
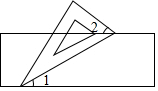 如图,小聪把一块含有60°角的直角三角形板的两个顶点放在直尺的对边上,并测得∠1=25°,则∠2的度数是( )
如图,小聪把一块含有60°角的直角三角形板的两个顶点放在直尺的对边上,并测得∠1=25°,则∠2的度数是( )| A. | 25° | B. | 30° | C. | 35° | D. | 60° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3.9×1010 | B. | 3.9×109 | C. | 0.39×1011 | D. | 39×109 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知AB是⊙O的直径,CD与⊙O相切于C,BE∥CO.
如图,已知AB是⊙O的直径,CD与⊙O相切于C,BE∥CO.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com