
如图,在平面直角坐标系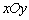 中,以点
中,以点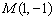 为圆心,以
为圆心,以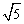 为半径作圆,与x轴交于A、B两点,与y轴交于C、D两点,二次函数
为半径作圆,与x轴交于A、B两点,与y轴交于C、D两点,二次函数 的图象经
的图象经
过点A、B、C,顶点为E.
(1)求此二次函数的表达式;
(2)设∠DBC=a,∠CBE=b,求sin(a-b)的值;
(3)坐标轴上是否存在点P,使得以P、A、C为顶点的三角形与△BCE相似.若存在,请直接写出点P的坐标;若不存在,请说明理由.
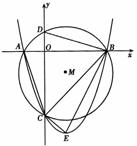
 解:(1)
解:(1)
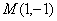 为圆心,半径为
为圆心,半径为
∴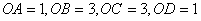
∴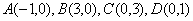
设二次函数的表达式为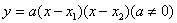
解得: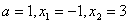
∴ 二次函数表达式为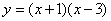
整理成一般式为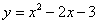
(2)过点E作EF⊥y轴于点F


∴可得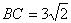
 点E为二次函数
点E为二次函数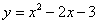 的顶点
的顶点
∴ 点E的坐标为
点E的坐标为
∴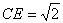

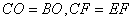
∴∠OCB=∠ECF=45º
∴∠BCE=90º
 在Rt△BCE中与Rt△BOD中,
在Rt△BCE中与Rt△BOD中,
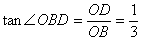 ,
,
∴∠CBE=∠OBD=b,
∴ sin(a-b)=sin(∠DBC-∠OBD)=sin∠OBC=
(3)显然 Rt△COA∽Rt△BCE,此时点P1(0,0)
过A作AP2⊥AC交y正半轴于P2,由Rt△CAP2 ∽Rt△BCE,得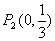
过C作CP3⊥AC交x正半轴于P3,由Rt△P3CA∽Rt△BCE,得P3(9,0)
故在坐标轴上存在三个点P1(0,0),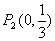 ,P3(9,0),使得以P、A、C为顶点的三角形与BCE相似
,P3(9,0),使得以P、A、C为顶点的三角形与BCE相似


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
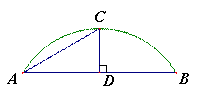
一件轮廓为圆形的文物出土后只留下了一块残片,文物学家希望能把此件文物进行
复原,因此把残片抽象成了一个弓形,如图所示,经过测量得到弓形高CD=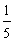 米,
米,
∠CAD=30°,请你帮助文物学家完成下面两项工作:
(1)作出此文物轮廓圆心O的位置(尺规作图,保留作图痕迹,不写作法);
(2)求出弓形所在圆的半径.
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
把多项式x4一8x2+16分解因式,所得结果是( ) (原创)
A.(x-2)2 (x+2)2 B. (x-4)2 (x+4)2 C.(x一4)2 D.(x-4)4
查看答案和解析>>
科目:初中数学 来源: 题型:
在一个不透明的盒子里装有6个分别写有数字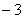 ,
,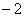 ,
,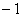 ,0,1,2,的小球,它们除数字不同外其余全部相同。现从盒子里随机取出一个小球,记下数字
,0,1,2,的小球,它们除数字不同外其余全部相同。现从盒子里随机取出一个小球,记下数字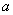 后不放回,再取出一个记下数字
后不放回,再取出一个记下数字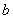 ,那么点
,那么点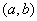 在抛物线
在抛物线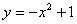 上的概率是( )
上的概率是( )
A.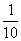 B.
B.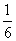 C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com