
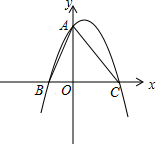
 如图,在平面直角坐标系中,二次函数y=-x2+x+6的图象与y轴交于点A,与x轴交于B,C两点(点B在点C的左侧),连接AB,AC.
如图,在平面直角坐标系中,二次函数y=-x2+x+6的图象与y轴交于点A,与x轴交于B,C两点(点B在点C的左侧),连接AB,AC.分析 (1)①令x=0和y=0可求得B、A与C的坐标,利用勾股定理求AC的长;
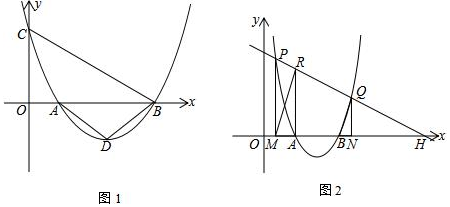
②如图1,作辅助线,构建直角△ABD,利用面积法求BD=2$\sqrt{5}$,利用勾股定理求AB的长,根据三角函数的定义可得结论;
(2)①利用勾股定理列方程求出H的坐标,横坐标是$\frac{1}{2}$,在抛物线的坐标轴上,如果不是,则不在;
②如图3,作辅助线,构建全等三角形,证明△APE≌△AC'F和△PAB′≌△C'AB',得∠AB'P=∠AB'C',再证明△AMN∽△AC'B',则$\frac{MN}{B'C'}=\frac{AM}{AC'}$=$\frac{AM}{AP}$,证P、E、M、A四点共圆,
得∠AMP=∠AEP=90°,所以△AMP是等腰直角三角形,则MN=$\frac{\sqrt{2}}{2}$B′C′,根据已知可得出结论.
解答 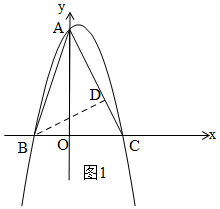 解:(1)①当x=0时,y=6,
解:(1)①当x=0时,y=6,
∴A(0,6),
∴OA=6,
当y=0时,-x2+x+6=0,
(x+2)(x-3)=0,
x=-2或3,
∵点B在点C的左侧,
∴B(-2,0),C(3,0),
∴OC=3,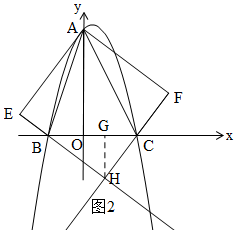
在Rt△AOC中,由勾股定理得:AC=$\sqrt{O{A}^{2}+O{C}^{2}}$=$\sqrt{{6}^{2}+{3}^{2}}$=3$\sqrt{5}$;
故答案为:(-2,0),(3,0),3$\sqrt{5}$;
②如图1,过B作BD⊥AC于D,则∠BDA=90°,
∵S△ABC=$\frac{1}{2}$BC•AO=$\frac{1}{2}$AC•BD,
即$\frac{1}{2}$×5×6=$\frac{1}{2}$×$3\sqrt{5}$×BD,
∴BD=2$\sqrt{5}$,
在Rt△AOB中,AB=$\sqrt{{2}^{2}+{6}^{2}}$=2$\sqrt{10}$,
∴sin∠BAC=$\frac{BD}{AB}$=$\frac{2\sqrt{5}}{2\sqrt{10}}$=$\frac{\sqrt{2}}{2}$;
(2)①如图2,过H作HG⊥x轴于G,
由折叠得:AE=AO=AF=6,∠E=∠AOB=90°,∠F=∠AOC=90°,
∠EAB=∠BAO,∠OAC=∠CAF,
∴∠EAF=2∠BAO+2∠OAC=2(∠BAO+∠OAC)=2∠BAC,
由(1)知:sin∠BAC=$\frac{\sqrt{2}}{2}$,且∠BAC为锐角,
∴∠BAC=45°,
∴∠EAF=∠E=∠F=90°,
∴四边形AEHF是正方形,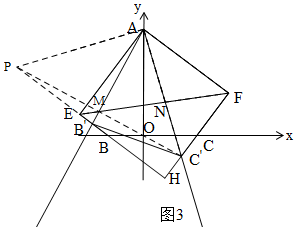
∴EH=FH=6,
设H(x,y),则OG=x,
∴BG=2+x,CG=3-x,
∵EB=OB=2,FC=OC=3,
∴BH=6-2=4,CH=6-3=3,
由勾股定理得:42-(2+x)2=32-(3-x)2,
x=$\frac{6}{5}$,
∴GH=$\sqrt{{3}^{2}-(3-\frac{6}{5})^{2}}$=$\frac{12}{5}$,
∴H($\frac{6}{5}$,-$\frac{12}{5}$);
∴点H不在抛物线对称轴上;
故答案为:($\frac{6}{5}$,-$\frac{12}{5}$);不在;
②如图3,延长B'E至P,使PE=C'F,连接AP,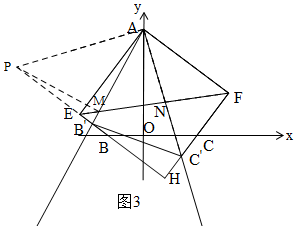
∵AE=AF,∠AEP=∠AFH=90°,
∴△APE≌△AC'F,
∴AP=AC',∠PAE=∠C'AF,
由旋转得:∠B′AC′=45°,
∴∠EAB′+∠C'AF=45°,
∴∠PAE+∠EAB′=45°,
∴∠PAB'=∠B'AC'=45°,
∵AB′=AB′,
∴△PAB′≌△C'AB',
∴∠AB'P=∠AB'C',
∵∠FEB'=∠B'AC'=45°,
∴∠EMB'=∠AC'B'=∠AMN,
∵∠MAN=∠B'AC',
∴△AMN∽△AC'B',
∴$\frac{MN}{B'C'}=\frac{AM}{AC'}$=$\frac{AM}{AP}$,
连接PM,
∵∠PAM=45°,∠PEM=90°+45°=135°,
∴∠PAM+∠PEM=180,
∴P、E、M、A四点共圆,
∴∠AMP=∠AEP=90°,
∴△AMP是等腰直角三角形,
∴$\frac{AM}{AP}$=$\frac{\sqrt{2}}{2}$,
∴$\frac{MN}{B'C'}$=$\frac{\sqrt{2}}{2}$,
∴MN=$\frac{\sqrt{2}}{2}$B′C′,
∵B′H2+C′H2=33=B'C'2,
∴B'C'=$\sqrt{33}$,
∴MN=$\frac{\sqrt{2}}{2}$×$\sqrt{33}$=$\frac{\sqrt{66}}{2}$.
故答案为:$\frac{\sqrt{66}}{2}$.
点评 本题是二次函数的综合题,考查了坐标轴的交点问题、勾股定理、等腰直角三角形的性质和判定、四点共圆的判定和性质、正方形的性质和判定、三角形相似的性质和判定等知识,当已知条件有平方和时,注意运用勾股定理的知识,构建直角三角形解决;本题是函数与几何变换的综合,有难度.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在△ABC中,AB=5,AC=3,BC=4,D是BC边上一动点,BE⊥AD,交其延长线于点E,EF⊥AC,交其延长线于点F,则AF的最大值为4.
如图,在△ABC中,AB=5,AC=3,BC=4,D是BC边上一动点,BE⊥AD,交其延长线于点E,EF⊥AC,交其延长线于点F,则AF的最大值为4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com