练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    9．如图，已知AD∥BE，∠1=∠2，请判断∠A与∠E是否相等？并说明理由．

    分析 首先根据∠1=∠2可得DE∥AC，进而得到∠E=∠EBC，再根据AD∥EB可得∠A=∠EBC，进而得到∠E=∠A．

    解答 解：∠A与=∠E，
    理由：∵AD∥BE，
    ∴∠A=∠3，
    又∵∠1=∠2，
    ∴DE∥AB，
    ∴∠E=∠3，
    ∴∠A=∠E．

    点评 此题主要考查了平行线的判定与性质，平行线的判定是由角的数量关系判断两直线的位置关系．平行线的性质是由平行关系来寻找角的数量关系．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    19．△ABC和△FED中，BD=FC，∠B=∠F．当添加条件AB=EF时，就可得到△ABC≌△FED，依据是SAS（只需填写一个你认为正确的条件）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    20．如果x2+2ax+16恰好是一个整式的完全平方，那么常数a=±4．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．计算
    （1）|-5|+$\sqrt{16}$-32．                    
    （2）2（a-1）-（2a-3）+3
    （3）$\sqrt{（-5）^{2}}$-|2-$\sqrt{2}$|-$\root{3}{-27}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．如图，在?ABCD中，E是AD边上的中点，连接BE并延长与CD的延长线交于点F．证明：AB=DF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    14．如图，三个相邻的正方形内接于半圆，若小正方形的面积为16cm2，则正方形BEFG的边长为（　　）
    A．4cmB．8cmC．4$\sqrt{5}$cmD．6$\sqrt{2}$cm

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

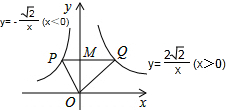    1．函数y=-$\frac{\sqrt{2}}{x}$（x＜0）和y=$\frac{2\sqrt{2}}{x}$（x＞0）的图象如图所示，O为坐标原点，M是y轴正半轴上任意一点，过点M作PQ∥x轴，分别与图中的函数图象相交于P、Q两点，连接OP、OQ，则△OPQ的面积为（　　）
    A．$\sqrt{2}$B．$\frac{3}{2}\sqrt{2}$C．2$\sqrt{2}$D．$\frac{5}{2}\sqrt{2}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    18．甲、乙两人5次射击命中的环数如下：
    甲798610
    乙78988
    则这两人5次射击命中的环数的平均数$\overline{{x}_{甲}}$=$\overline{{x}_{乙}}$=8，方差S甲2（　　）S乙2．
    A．＞B．＜C．=D．以上都不对

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．已知$\left\{\begin{array}{l}{x=1}\\{y=-1}\end{array}\right.$是方程组$\left\{\begin{array}{l}{3x+2y=b}\\{4x-2y=2a-1}\end{array}\right.$的解，求a、b的值．

    查看答案和解析>>

    同步练习册答案